李宏毅机器学习课程笔记-4.2分类模型之概率生成模型

Posted on | | Visitors:
Words count in article: 1,741 字 | Reading time ≈ 7 分

贝叶斯公式

$P(A\cap B)=P(A)P(B|A)=P(B)P(A|B)$

$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$

全概率公式

$P(B)=\sum_{i=1}^nP(A_i)P(B|A_i)$

概率生成模型（Probalitity Generative Model）

理论与定义

假设有两个类别$C_1$和$C_2$，要判断对象$x$属于哪个类别，即计算$x$属于类别$C_1$的概率，这样把分类问题变成了概率计算问题。

  1. 根据贝叶斯公式（Bayes’ theorem）和全概率公式（Total Probability Theorem）可以知道，$x$属于类别$C_1$的概率为$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x)}=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}$，如果$P(C_1|x)>0.5$则类别为$C_1$，否则类别为$C_2$。

  2. 概率生成模型的意思就是可以通过这个模型生成一个$x$。

    具体来讲就是，根据$P(x)=P(x|C_1)P(C_1)+P(x|C_2)P(C_2)$计算出$P(x)$，就可以知道$x$的分布进而生成$x$。如果想要计算出$P(x)$，就要根据训练集估计出$P(C_1)$、$P(x|C_1)$、$P(C_2)$、$P(x|C_2)$这四个值。

    更直观一点地讲，每个类别就是一个多元正态分布，其中多元是因为每个样本有多个维度的特征。

  3. 可以根据数据集中属于两个类别的对象的数量计算$P(C_1)$和$P(C_2)$这两个先验概率（Prior Probability）。

    如果有2个样本属于类别$C_1$，4个样本属于类别$C_2$，那$P(C_1)=\frac{1}{3}$、$P(C_2)=\frac{2}{3}$。

  4. 要计算后验概率（Posterior Probability）$P(x|C_1)$和$P(x|C_2)$，可以假设训练集中的各类别样本的特征分别是从某个多元正态分布（多元对应特征的多维）中取样得到的，或者说是假设训练集中各类别样本的特征分别符合某多元正态分布。

    该正态分布的输入是一个样本的特征$x$，输出为样本$x$是从这个正态分布取样得到（或者说该样本属于某类别）的概率密度，然后通过积分就可以求得$P(x|C_1)$和$P(x|C_2)$。

  5. 正态分布公式为$f_{\mu,\Sigma}(x)=\frac{1}{(2\pi)^{\frac{D}{2}}}\frac{1}{|\Sigma|^{\frac{1}{2}}}e^{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)}$。

    正态分布有2个参数，即均值$\mu$（代表正态分布的中心位置）和协方差矩阵（Covariance Matrix）$\Sigma$（代表正态分布的离散程度），计算出均值$\mu$和协方差$\Sigma$即可得到该正态分布。

    公式中的$D$为多维特征的维度。

  6. 实际上从任何一个正态分布中取样都有可能得到训练集中的特征，只是概率不同而已。通过极大似然估计（Maximum Likelihood Estimate，MLE），我们可以找到取样得到训练集特征的概率最大的那个正态分布，假设其均值和协方差矩阵为$\mu^$和$\Sigma^$。

    1. 根据某正态分布的均值$\mu$和协方差$\Sigma$，可以计算出从该正态分布取样得到训练集的概率。$L(\mu,\Sigma)=f_{\mu,\Sigma}(x^1)f_{\mu,\Sigma}(x^2)\dots f_{\mu,\Sigma}(x^N)$，这就是似然函数（Likelihood Function），其中$N$是训练集中某个类别样本的数量。

    2. $\mu^,\Sigma^=arg\ max_{\mu,\Sigma}L(\mu,\Sigma)$。

      当然可以求导。

      直觉：$\mu^=\frac{1}{N}\sum_{i=1}^Nx^i$，$\Sigma^=\frac{1}{N}\sum_{i=1}^N(x^i-\mu^)(x^i-\mu^)T$。

协方差矩阵共享

每个类别的特征符合一个多元正态分布，每个多元正态分布也有不同的均值和协方差矩阵。让每个类别对应的多元正态分布共享一个协方差矩阵（各个协方差矩阵的加权平均和），公式为$\Sigma=\frac{N_1}{N_1+N_2}\Sigma^1+\frac{N_2}{N_1+N_2}\Sigma^2$，可以减少模型参数，缓解过拟合。

极大似然估计

  • 定义

    极大似然估计指已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，然后通过若干次试验，观察其结果，利用结果推出参数的大概值。一般说来，在一次试验中如果事件A发生了，则认为此时的参数值会使得$P(A|\theta)$最大，极大似然估计法就是要这样估计出的参数值，使所选取的样本在被选的总体中出现的可能性为最大。

  • 求极大似然函数估计值的一般步骤：

    1. 写出似然函数
    2. 对似然函数取对数，并整理
    3. 求导数
    4. 解似然方程

  • 当共享协方差矩阵时

    此时似然函数是$L(\mu^1,\mu^2,\Sigma)=f_{\mu^1,\Sigma}(x^1)f_{\mu^2,\Sigma}(x^2)\dots f_{\mu^1,\Sigma}(x^{N_1})\times f_{\mu^2,\Sigma}(x^{N_1+1})f_{\mu^2,\Sigma}(x^{N_1+2})\dots f_{\mu^2,\Sigma}(x^{N_1+N_2})$，其中$N_1$为训练集中类别$C_1$的样本数、$N_2$为训练集中类别$C_2$的样本数。

    当只有两个类别、两个特征时，如果共享协方差矩阵，那最终得到的两个类别的分界线是直线（横纵轴是两个特征），这一点可以在下文解释。

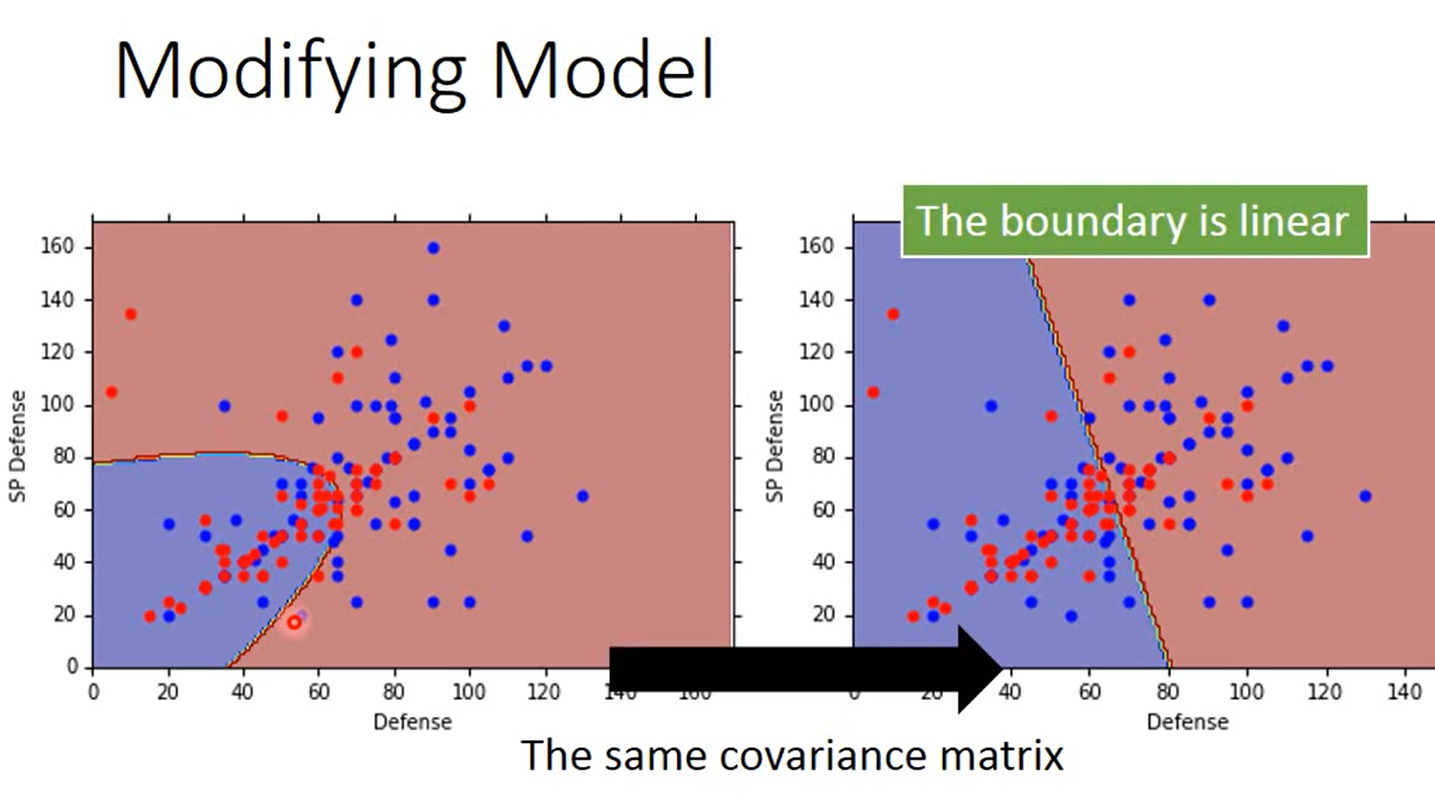
    ClassificationLinearBoundary.png

  • 除了正态分布，还可以用其它的概率模型。

    比如对于二值特征，可以使用伯努利分布（Bernouli Distribution）。

  • 朴素贝叶斯分类

    如果假设样本各个维度的数据是互相独立的，那这就是朴素贝叶斯分类器（Naive Bayes Classfier）。

Sigmoid函数

由上面我们知道$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}$，

令$z=ln\frac{P(x|C_1P(C_1)}{P(x|C_2P(C_2))}$，则$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1)+P(x|C_2)P(C_2)}=\frac{1}{1+\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1)}}=\frac{1}{1+e^{-z}}=\sigma(z)$，这就是Sigmoid函数。

如果共享协方差矩阵，经过运算可以得到$z=w^T\cdot x+b$的形式，其中常量$w^T=(\mu^1-\mu^2)^T\Sigma^{-1}$，常量$b=-\frac{1}{2}(\mu^1)^T(\Sigma^1)^{-1}\mu^1+\frac{1}{2}(\mu^2)^T(\Sigma^2)^{-1}\mu^2+ln\frac{N_1}{N_2}$，即形如$P(C_1|x)=\sigma(w\cdot x+b)$。

我们最终得到了一个这么简单的一个式子，有一个问题是，我们假设了分布、用了一堆概率，为什么不能直接定义线性模型呢？该问题的答案在下一篇文章李宏毅机器学习课程笔记-4.3分类模型之逻辑回归中的判别模型VS生成模型部分。

Github（github.com）：@chouxianyu

Github Pages（github.io）：@臭咸鱼

知乎（zhihu.com）：@臭咸鱼

博客园（cnblogs.com）：@臭咸鱼

B站（bilibili.com）：@绝版臭咸鱼

微信公众号：@臭咸鱼

转载请注明出处，欢迎讨论和交流!