逻辑回归
假设训练集如下,有2个类别$C_1$和$C_2$,表格中的每列为一个样本。
例如,第一列表示样本$x^1$的类别为$C_1$,所以它的标签$\hat y^1$是1。
| $x^1$ | $x^2$ | $x^2$ | $\dots$ | $x^N$ |
|---|---|---|---|---|
| $C_1$ | $C_1$ | $C_2$ | $\dots$ | $C_1$ |
| $\hat y^1=1$ | $\hat y^2=1$ | $\hat y^3=0$ | $\dots$ | $\hat y^N=1$ |
模型定义
在分类(Classification)一节中,我们要找到一个模型$P_{w,b}(C_1|x)$,如果$P_{w,b}(C_1|x)\geq0.5$,则$x$属于类别$C_1$,否则属于类别$C_2$。
可知$P_{w,b}(C_1|x)=\sigma(z)$,其中$\sigma(z)=\frac{1}{1+e^{-z}}$(Sigmoid Function),$z=w\cdot x+b=\sum_{i=1}^Nw_ix_i+b$。
最终我们找到了模型$f_{w,b}(x)=\sigma(\sum_{i=1}^Nw_ix_i+b)$,这其实就是逻辑回归(Logistic Regression)。
损失函数
从模型$f_{w,b}(x)=P_{w,b}(C_1|x)$中取样得到训练集的概率为:$L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\dots f_{w,b}(x^N)$(似然函数)。
我们要求$w^,b^=arg\ max_{w,b}L(w,b)$,等同于$w^,b^=arg\ min_{w,b}-lnL(w,b)$(对数似然方程,Log-likelihood Equation)。
而$-lnL(w,b)=-lnf_{w,b}(x^1)-lnf_{w,b}(x^2)-ln(1-f_{w,b}(x^3))\dots$,其中$lnf_{w,b}(x^n)=\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f(x^n))$,所以$-lnL(w,b)=\sum_{n=1}^N-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))]$,式中$n$用来选择某个样本。
假设有两个伯努利分布$p$和$q$,在$p$中有$p(x=1)=\hat y^n,p(x=0)=1-\hat y^n$,在$q$中有$q(x=1)=f(x^n),q(x=0)=1-f(x^n)$,则$p$和$q$的交叉熵(Cross Entropy,代表两个分布有多接近,两个分布一模一样时交叉熵为0)为$H(p,q)=-\sum_xp(x)ln(q(x))$。
所以损失函数$L(f)=\sum_{n=1}^NC(f(x^n),\hat y^n)$,其中$C(f(x^n),\hat y^n)=-[\hat y^nlnf_{w,b}(x^n)+(1-\hat y^n)ln(1-f_{w,b}(x^n))]$,即损失函数为所有样本的$f(x^n)$与$\hat y^n$的交叉熵之和,式中$n$用来选择某个样本。
梯度
$\frac{-lnL(w,b)}{\partial w_i}=\sum_{n=1}^{N}-(\hat y^n-f_{w,b}(x^n))x_i^n$(推导过程省略,具体见李宏毅机器学习视频14分56秒),其中$i$用来选择数据的某个维度,$n$用来选择某个样本,$N$为数据集中样本个数。
该式表明,预测值与label相差越大时,参数更新的步幅越大,这符合常理。
逻辑回归VS线性回归

模型
逻辑回归模型比线性回归模型多了一个sigmoid函数;
逻辑回归输出是[0,1],而线性回归的输出是任意值。
损失函数
逻辑回归模型使用的训练集中label的值必须是0或1,而线性回归模型训练集中label的值是真实值。
图中线性回归损失函数中的$\frac{1}{2}$是为了方便求导
这里有一个问题,为什么逻辑回归模型中不使用Square Error呢?这个问题的答案见下文
梯度
逻辑回归模型和线性回归模型的梯度公式一样
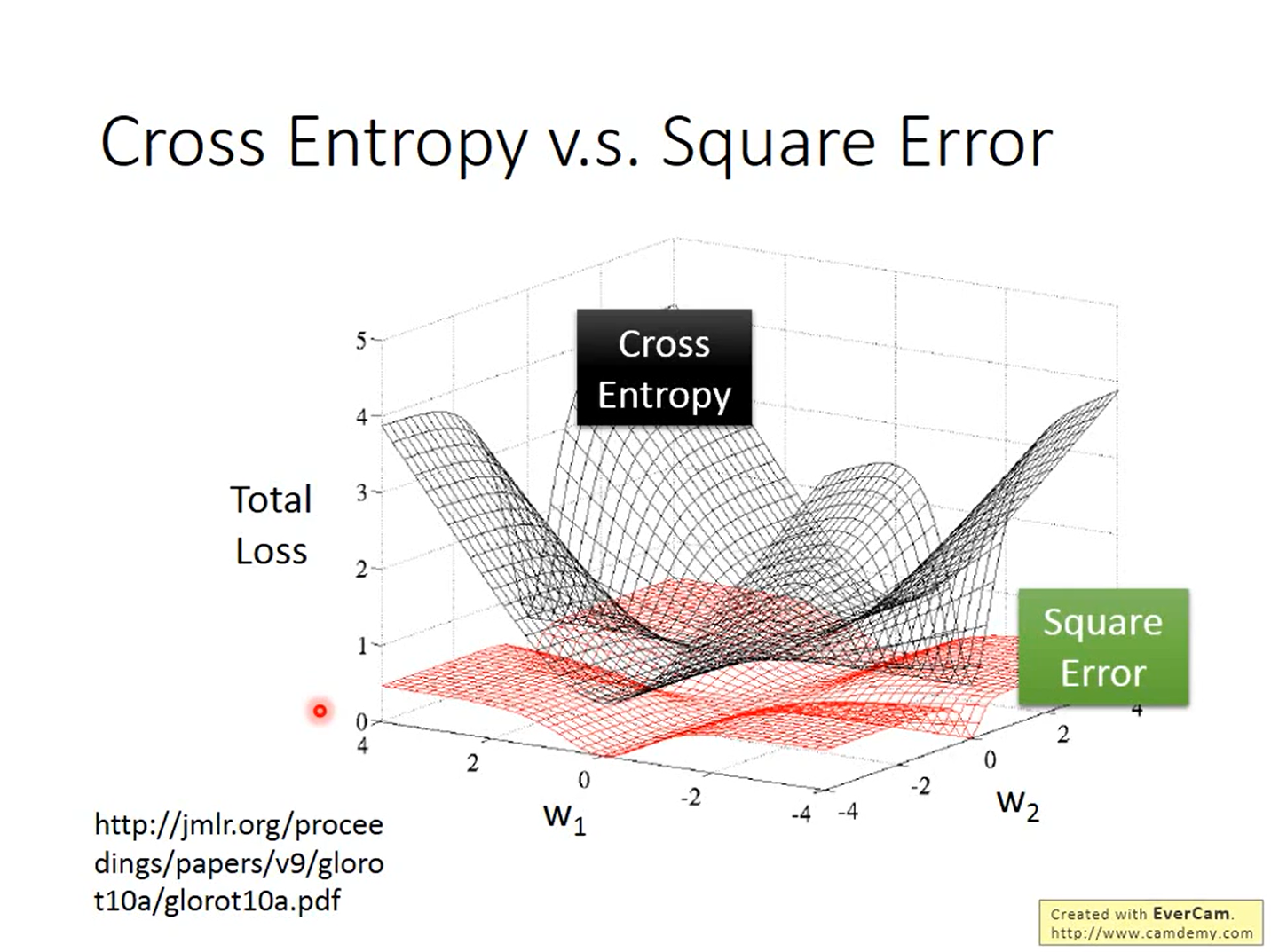
为什么逻辑回归模型中不使用Square Error

由上图可知,当label的值为1时,不管预测值是0还是1,梯度都为0,当label值为0时也是这样。
如下图所示,如果在逻辑回归中使用Square Error,当梯度接近0时,我们无法判断目前与最优解的距离,也就无法调节学习率;并且在大多数时候梯度都是接近0的,收敛速度会很慢。
判别模型VS生成模型
形式对比
逻辑回归是一个判别模型(Discriminative Model),用正态分布描述后验概率(Posterior Probability)则是生成模型(Generative Model)。
如果生成模型中共用协方差矩阵,那两个模型/函数集其实是一样的,都是$P(C_1|x)=\sigma(w\cdot x+b)$。
因为做了不同的假设,即使是使用同一个数据集、同一个模型,找到的函数是不一样的。
优劣对比
- 如果现在数据很少,当假设了概率分布之后,就可以需要更少的数据用于训练,受数据影响较小;而判别模型就只根据数据来学习,易受数据影响,需要更多数据。
- 当假设了概率分布之后,生成模型受数据影响较小,对噪声的鲁棒性更强。
- 对于生成模型来讲,先验的和基于类别的概率(Priors and class-dependent probabilities),即$P(C_1)$和$P(C_2)$,可以从不同的来源估计得到。以语音识别为例,如果使用生成模型,可能并不需要声音的数据,网上的文本也可以用来估计某段文本出现的概率。
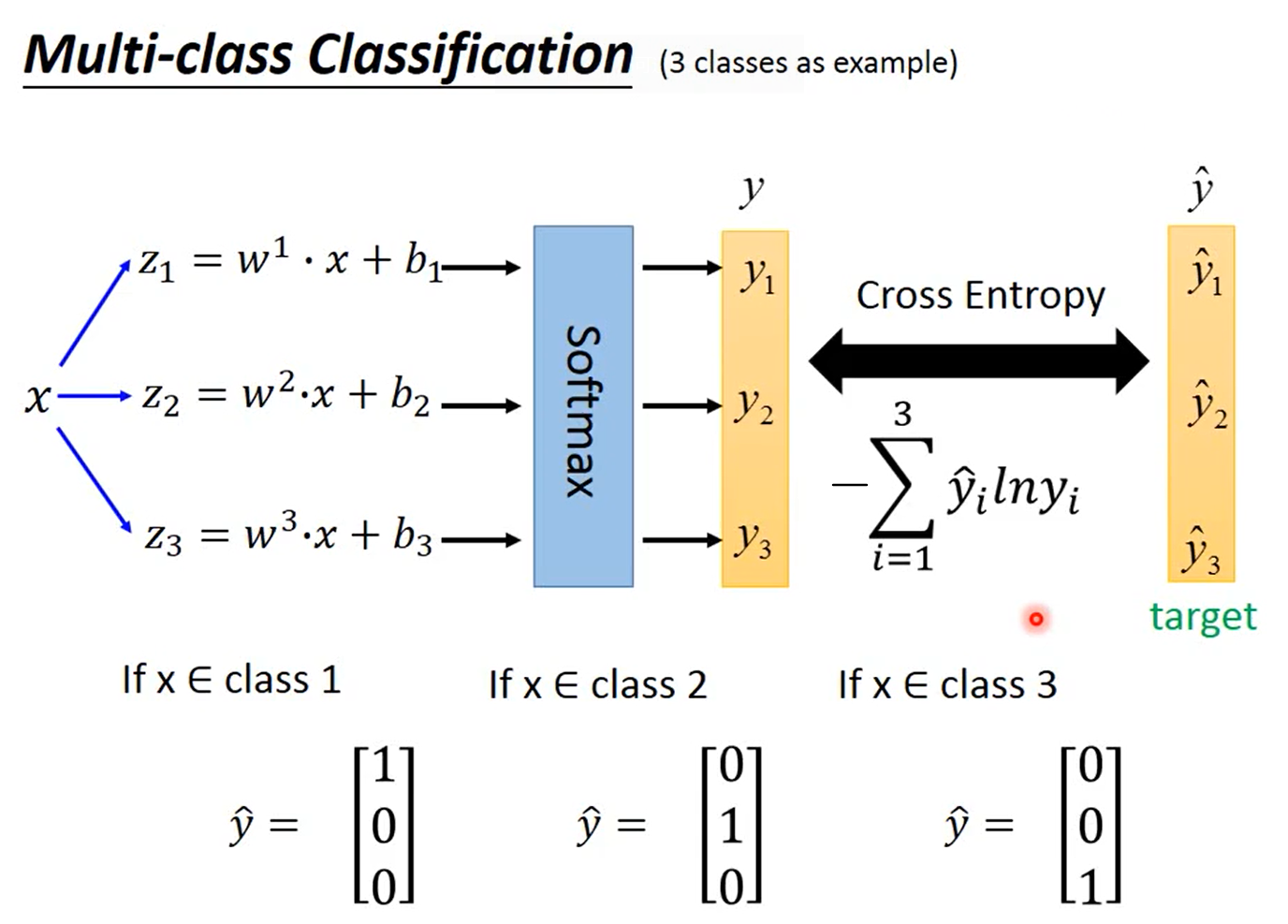
多分类(Multi-class Classification)
以3个类别$C_1$、$C_2$和$C_3$为例,分别对应参数$w^1,b_1$、$w^2,b_2$和$w^3,b_3$,即$z_1=w^1\cdot x+b_1$、$z_2=w^2\cdot x+b_2$和$z_3=w^3\cdot x+b_3$。
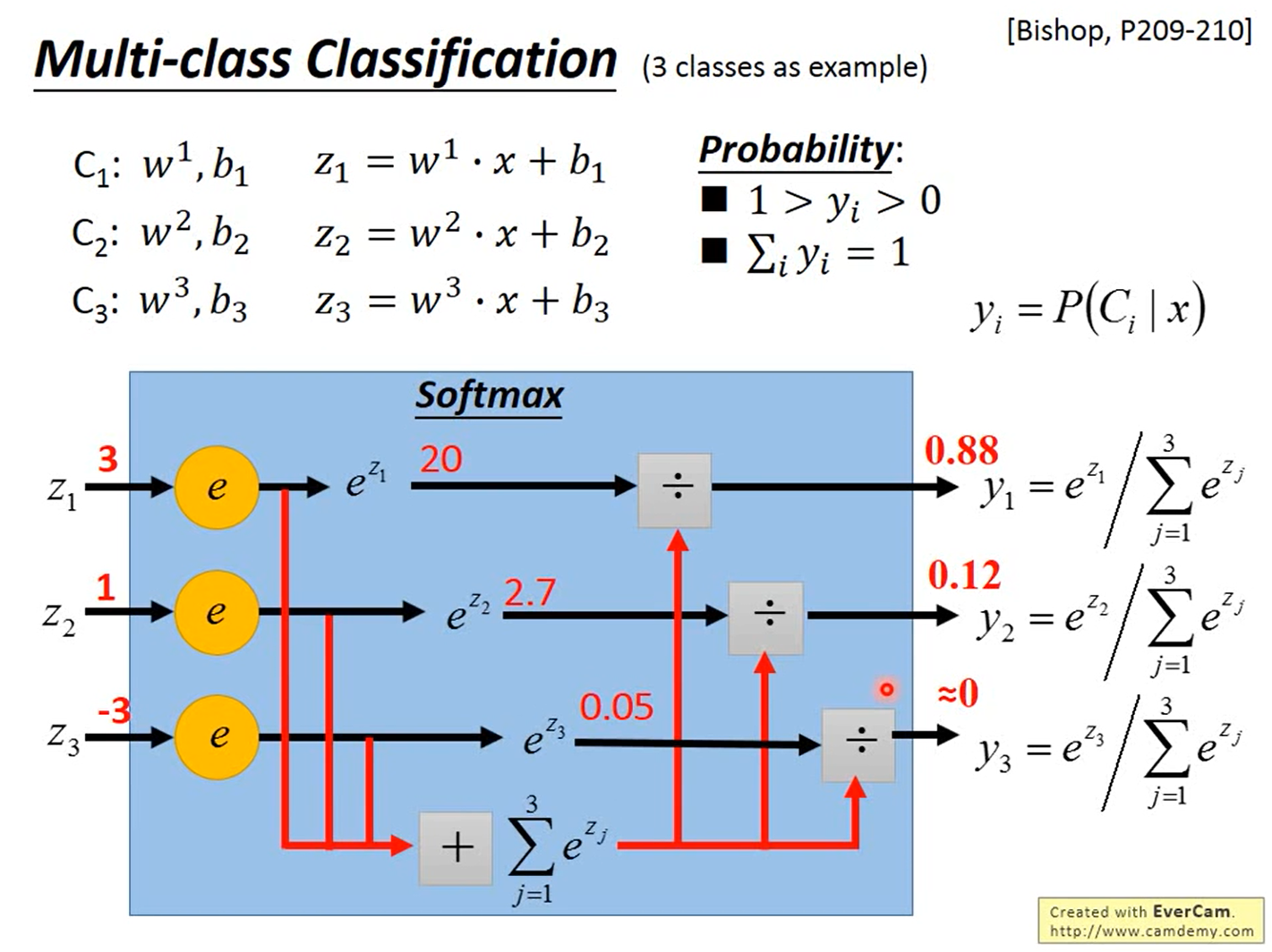
Softmax
使用Softmax($y_i=\frac{e^{z_i}}{\sum_{j=1}^3e^{z_j}}$),使得$0<y_i<1$以及$\sum_{i=1}^3y_i=1$,其中$y_i=P(C_i|x)$,即一个样本$x$属于类别$C_i$的概率不超过1,属于所有类别的概率之和为1。==Softmax公式中的z是一个参数吗?怎么确定或求得?==
Softmax公式中为什么要用$e$?这是有原因/可解释的,可以看下PRML,也可以搜下最大熵。
最大熵(Maximum Entropy)其实也是一种分类器,和逻辑回归一样,只是从信息论的角度来看待。
损失函数
计算预测值$y$和$\hat y$的交叉熵,$y$和$\hat y$都是一个向量,即$-\sum_{i=1}^3\hat y^ilny^i$。
这时需要使用one-hot编码:如果$x\in C_1$,则$y=\begin{bmatrix}1\\0\\0\end{bmatrix}$;如果$x\in C_2$,则$y=\begin{bmatrix}0\\1\\0\end{bmatrix}$;如果$x\in C_3$,则$y=\begin{bmatrix}0\\0\\1\end{bmatrix}$。
梯度
和逻辑回归的思路一样。
逻辑回归的局限
如下图所示,假如有2个类别,数据集中有4个样本,每个样本有2维特征,将这4个样本画在图上。
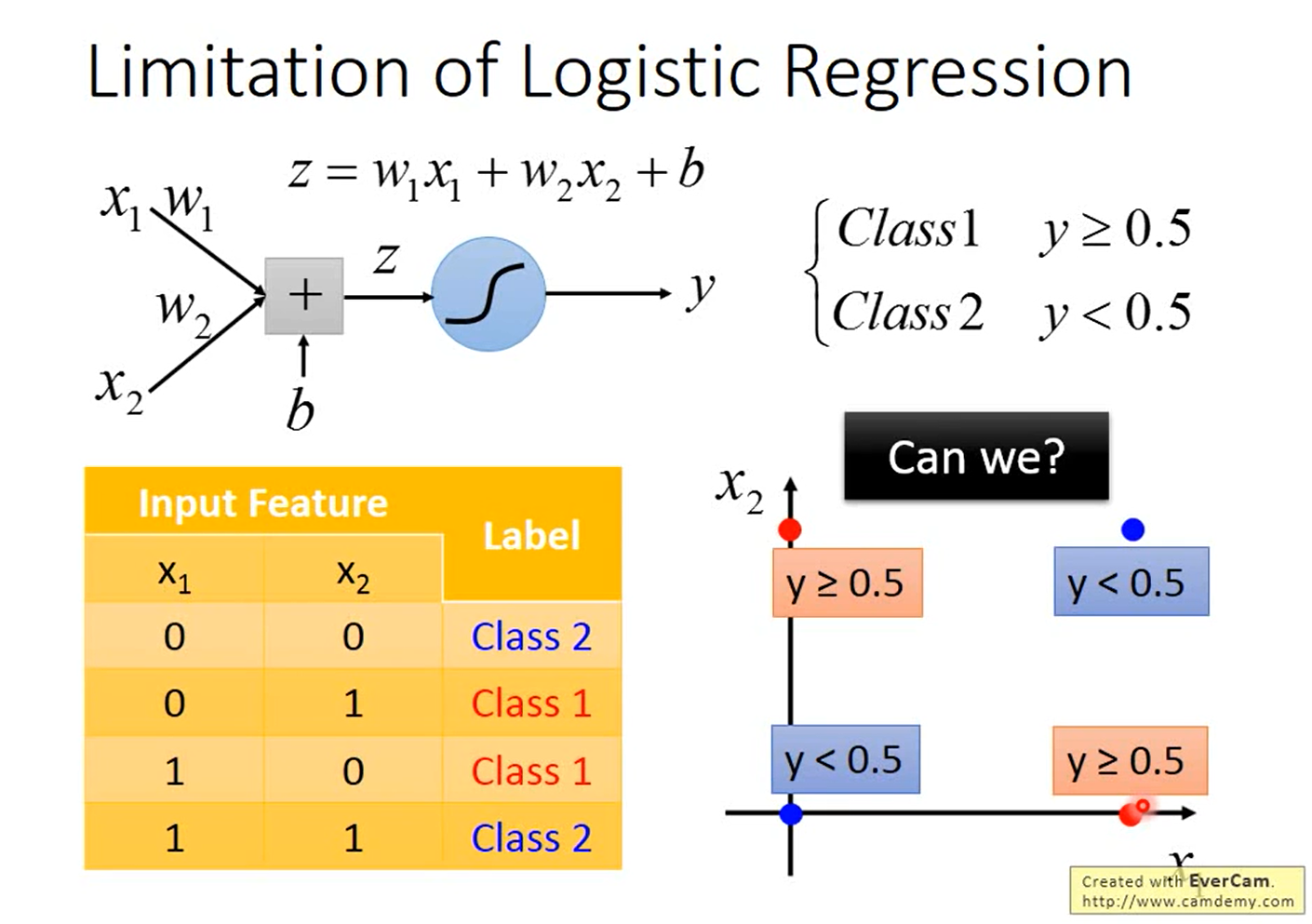
如下图所示,假如用逻辑回归做分类,即$y=\sigma(z)=\sigma(w_1x_1+w_2x_2+b)$,我们找不到一个可以把“蓝色”样本和“红色”样本间隔开的函数。
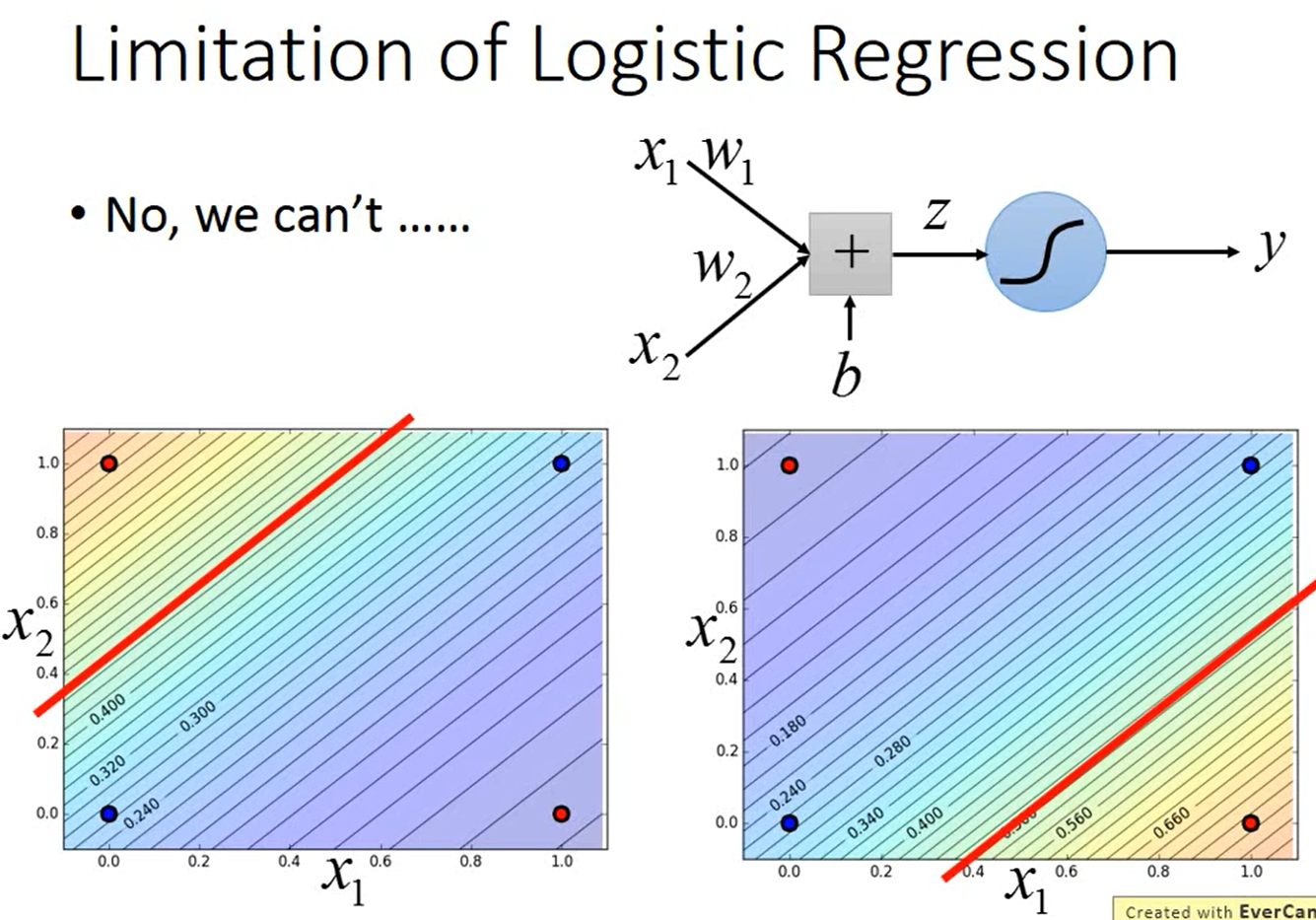
假如一定要用逻辑回归,那我们可以怎么办呢?我们可以尝试特征变换(Feature Transformation)。
特征变换(Feature Transformation)
在上面的例子中,我们并不能找到一个能将蓝色样本和红色样本间隔开的函数。
如下图所示,我们可以把原始的数据/特征转换到另外一个空间,在这个新的特征空间中,找到一个函数将“蓝色”样本和“红色”样本间隔开。
比如把原始的两维特征变换为与$\begin{bmatrix}0\\0\end{bmatrix}$和$\begin{bmatrix}1\\1\end{bmatrix}$的距离,在这个新的特征空间中,“蓝色”样本和“红色”样本是可分的。
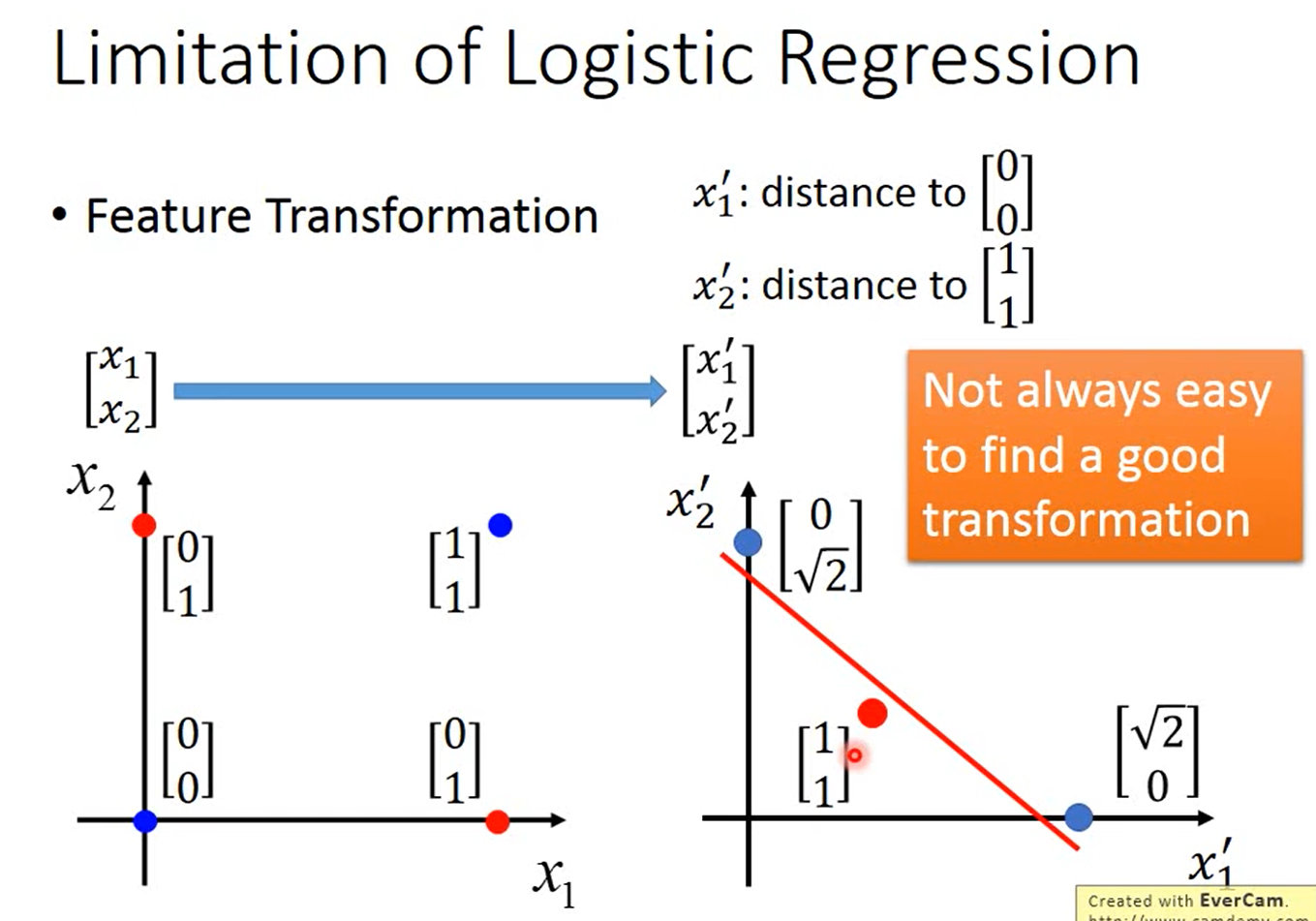
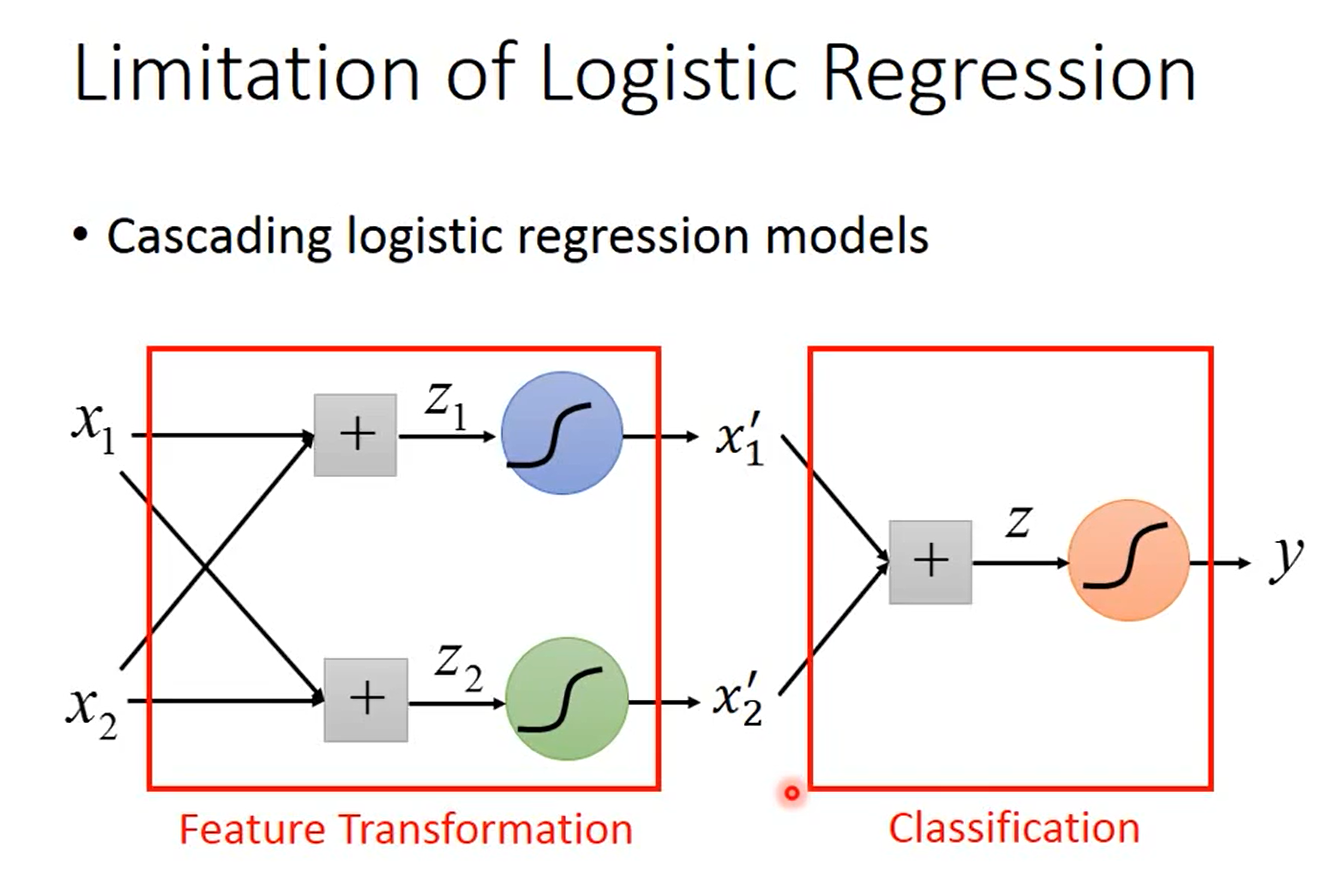
但有一个问题是,我们并不一定知道怎么进行特征变换。或者说我们想让机器自己学会特征变换,这可以通过级联逻辑回归模型实现,即把多个逻辑回归模型连接起来,如下图所示。
下图中有3个逻辑回归模型,根据颜色称它们为小蓝、小绿和小红。小蓝和小绿的作用是分别将原始的2维特征变换为新的特征$x_1’$和$x_2’$,小红的作用是在新的特征空间$\begin{bmatrix}x_1’\\x_2’\end{bmatrix}$上将样本分类。
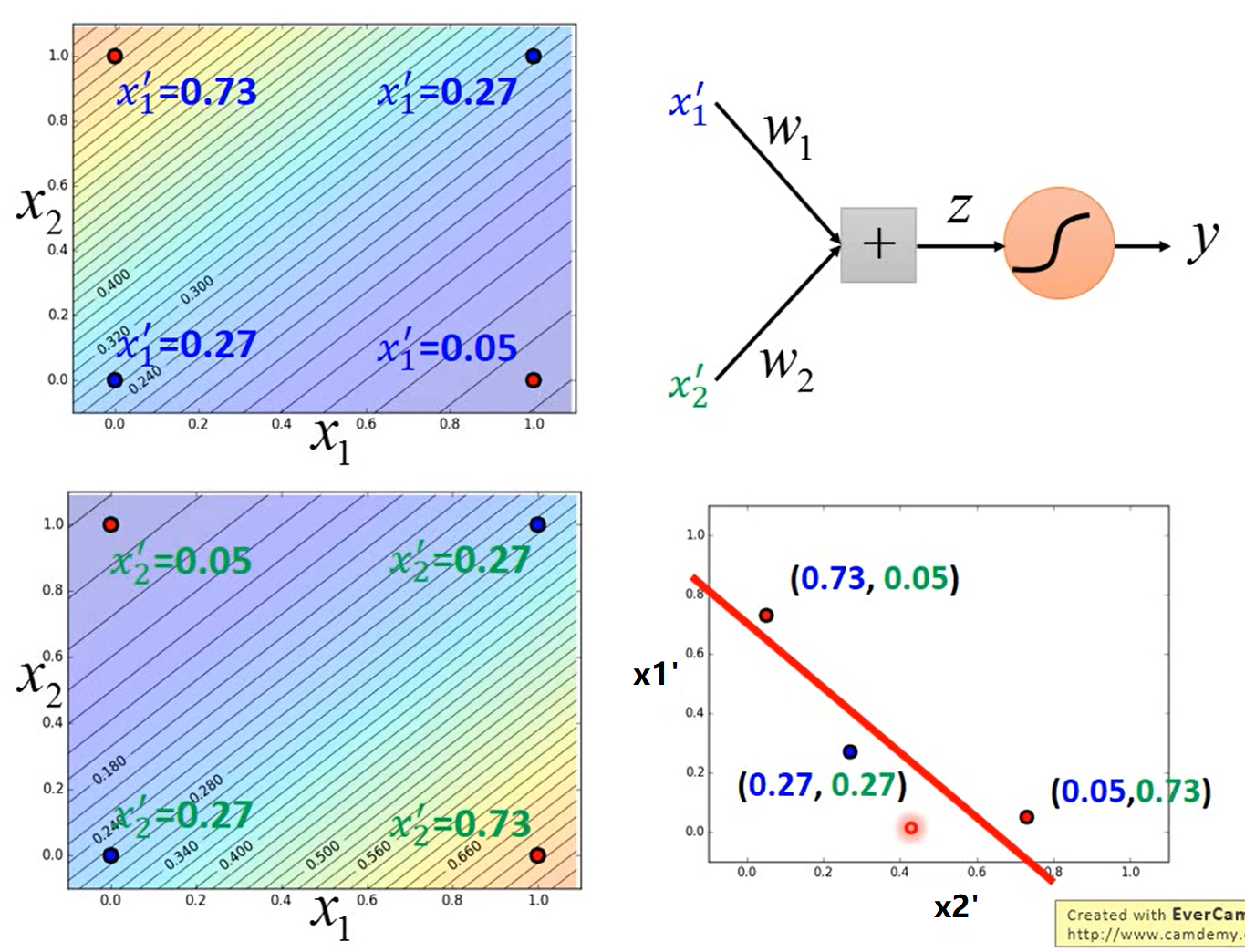
如下图所示,举一个例子。小蓝的功能是(下图左上角),离$(1,0)$越远、离$(0,1)$越近,则$x_1’$越大;小蓝的功能是(下图左下角),离$(1,0)$越远、离$(0,1)$越近,则$x_2’$越小。小蓝和小绿将特征映射到新的特征空间$\begin{bmatrix}x_1’\\x_2’\end{bmatrix}$中,结果见下图右下角,然后小红就能找到一个函数将“蓝色”样本和“红色”样本间隔开。
神经网络(Neural Network)
假如把上例中的一个逻辑回归叫做神经元(Neuron),那我们就形成了一个神经网络。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!