传染病模型

Posted on | | Visitors:
Words count in article: 300 字 | Reading time ≈ 1 分

简介

该模型在数学建模中可以解决很多问题。

该模型由三个微分方程构成。

建立模型

定义变量

假设系统中有三种人：

  • 易感染的人

    数量用$S$表示，刚开始所有人都是易感染的人

  • 感染的人

    数量用$I$表示

  • 康复的人

    数量用$R$表示（假设该传染病不致命）

微分方程

$\begin{equation}
\left\{
\begin{array}{r1}
\frac{dS}{dt}=-\beta SI\\
\frac{dI}{dt}=\beta SI-\gamma I\\
\frac{dR}{dt}=\gamma I\\
\end{array}
\right.
\end{equation}$

其中$\beta$是接触率，$\gamma$是康复率。

代码

函数odesir

1
2
3
4
5
6
7
8
9
function dy = odesir(t, y, beta, gamma)
% 根据传染病模型者中的y和t求出dy/dt
% y=[S; I; R]
dy =
[
	-beta*y(1)*y(2); % dS/dt
	beta*y(1)*y(2) - gamma*y(2); % dS/dt
	gamma*y(2); % dR/dt
]

计算

1
2
3
4
5
6
7
8
9
10
N = 100;
beta = 0.01;
gamma = 0.1;
tspan = [0,50];
y0 = [99,1,0];
[t y] = ode45(@odesir, tspan, y0, [], bata, gamma);
plot(t,y);
xlabel('time');
ylabel('population');
legend('S', 'I', 'R');

ode23和ode45的区别：精度不一样，ode45精度高。

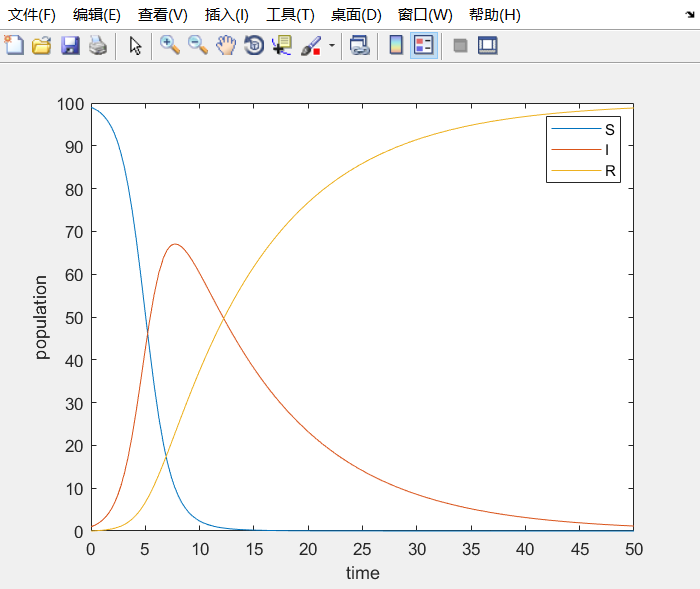
结果

传染病.png

作者：@臭咸鱼

本文为作者原创，转载请注明出处：https://chouxianyu.github.io

欢迎讨论和交流!