无监督学习(Unsupervised Learning)可以分为两类:
- 化繁为简
- 聚类(Clustering)
- 降维(Dimension Reduction)
- 无中生有
- 生成(Generation)
在无监督学习(Unsupervised Learning)中,数据集中通常只有$(x,\hat y)$中的$x$或$\hat y$,其中:
- 化繁为简就是把复杂的input变成比较简单的output,比如把一堆未标注的“树”图片转变为一棵抽象的“树”,此时数据集只有input $x$,而没有output $\hat y$。
- 无中生有就是随机给模型一个输入(比如是一个数字),它就会生成不同图像,此时数据集中没有input $x$,而只有output $\hat y$
聚类
定义
聚类(clustering)就是把”相近“的样本划分为同一类,比如用聚类算法对一些没有标签的图片进行分类,然后人工为这些类别打上cluster 1、cluster 2、cluster 3的标签。
一个critical的open question
在聚类算法中要分几个cluster?不能太多也不能太少,需要empirically决定。
聚类算法的缺点
它强迫每个样本属于并只属于1个cluster,实际上一个样本可能拥有多个cluster的特征,如果强制把它划分到某个cluster,就会失去很多信息。
如果原先的object是high dimension的,比如image,那现在用它的属性来描述自身,就可以使之从高维空间转变为低维空间,这就是所谓的降维(Dimension Reduction)
K-means
最常用的聚类方法是K-means,其目标为将N个无标签样本$\{x^1,…,x^n,…,x^N\}$划分为K个cluster,其算法流程如下:
初始化K个cluster的center:$c^i,i\in \{1,2,…,K\}$
初始化方法可以是从N个样本中随机选取K个样本作为K个center $c^i$的初始值;
如果不从样本中选取center的初始值,最终可能会导致部分cluster中没有样本。
遍历所有样本$x^n$并判断它属于哪个cluster
如果$x^n$与第i个cluster的center $c^i$最“接近”,那$x^n$就属于该cluster;
我们用$b_i^n=1$表示样本$x^n$属于第i个cluster,$b_i^n=0$表示不属于。
更新center:把每个cluster里的所有object取平均值作为新的center值,即$c^i=\sum\limits_{x^n}b_i^n x^n/\sum\limits_{x^n} b_i^n$
反复第2步和第3步
HAC
HAC的全称是Hierarchical Agglomerative Clustering,它是一种层次聚类算法
假设有5个样本,想要通过HAC进行聚类,其步骤为:
build a tree:
过程与哈夫曼树的建树过程类似,只不过哈夫曼树是依据词频建树,而HAC是依据样本相似度建树。
对于所有样本,两两计算相似度并挑出最相似的2个样本,比如样本1和2,将样本点1和2进行merge(比如可以对两个vector取平均)得到代表这2个样本的新“样本”,此时只剩下4个样本,再重复上述步骤合并样本直到只剩下一个样本
pick a threshold
选取相似度阈值,形象来讲就是在已构造的tree上横着切一刀,切到的每个“树枝”就是1个cluster,如下图所示。
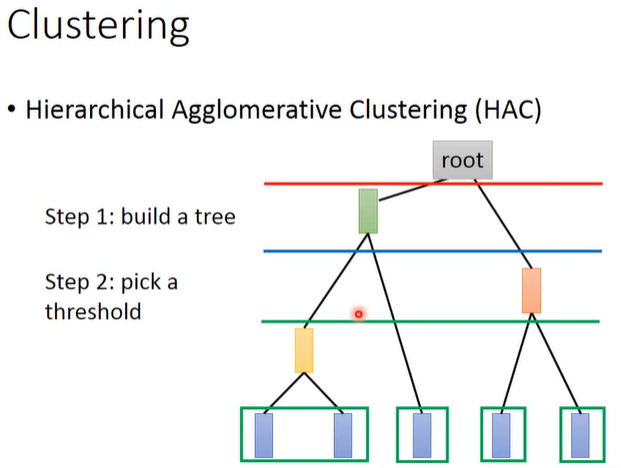
HAC和K-means的最大区别在于如何决定cluster的数量。K-means中需要人工确定cluster数量,而HAC中需要人工确定相似度阈值。
降维
降维即Dimension Reduction。
引入降维
聚类算法的假设是每个样本属于并只属于1个cluster,但实际上一个样本可能拥有多个cluster的特征,如果强制把它划分到某个cluster,就会失去很多信息。所以可以用一个vector来描述1个样本,该vector的每一维表示样本的某一种属性,这种做法就叫Distributed Representation/Dimension Reduction。
降维作用原理
因为数据存在冗余。比如MNIST手写数字图片是28×28的matrix,反过来想,一个任意的28×28的matrix转成图片看起来应该都不会是个数字,或许我们并不需要这么大的数据量来描述数字。
如何实现降维
Dimension Reduction就是要找一个function,其输入是原始的高维特征$x$,其输出是降维后的低维特征$z$,其中$z$的维度数比$x$少。
最简单的Dimension Reduction是Feature Selection,即直接将高维数据中一些直观上认为无效的维度删除,这样就做到了降维。但Feature Selection不总是有用,因为很多情况下每个维度其实都不能被直接删除,甚至我们不知道哪些维度可以删除哪些维度不可以删除。
生成
略
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!