生成模型中的半监督学习:Semi-supervised Learning for Generative Model
有监督生成模型
有监督生成模型:Supervised Generative Model
如下图所示,在有监督生成模型中,得到$P(C_1),P(C_2),\mu^1,\mu^2,\Sigma$后,就可以计算出$x$属于类别$C_i$的概率$P(C_i|x)$。

半监督生成模型
半监督生成模型:Semi-supervised Generative Model
基于有监督生成模型,当有了无标签数据之后(下图中绿色圆点),我们会明显发现有监督生成模型中的$P(C_1),P(C_2),\mu^1,\mu^2,\Sigma$并不够正确,比如2个类别的分布应该接近于下图中虚线圆圈、先验概率$P(C_1)$应该小于$P(C_2)$,所以应该使用无标签数据重新估计$P(C_1),P(C_2),\mu^1,\mu^2,\Sigma$。
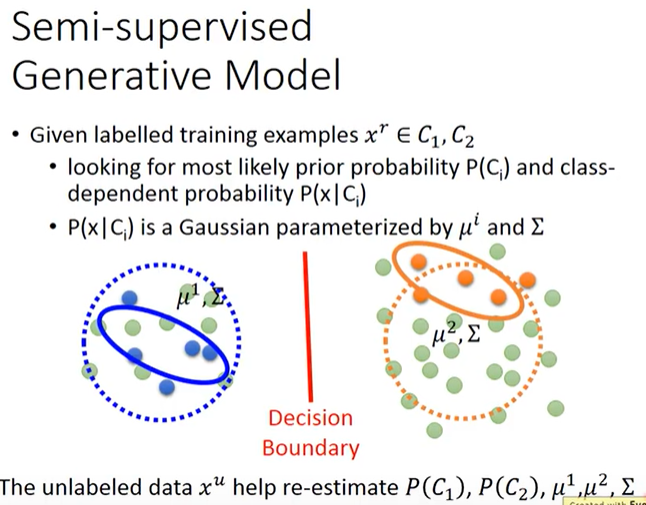
直观理解
具体来讲,按照以下步骤进行计算:
初始化参数:$\theta=\{P(C_1),P(C_2),\mu^1,\mu^2,\Sigma\}$
可以随机初始化,也可以用有标签数据估算
通过$\theta$计算每个样本$x^u$属于类别$C_i$的概率$P_\theta(C_i|x^u)$
更新参数$\theta$(其实重点就是如何同时利用有标签数据和无标签数据实现半监督)
- $P(C_1)=\frac{N_1+\sum_{x^u}P(C_1|x^u)}{N}$,其中$N$是所有样本的数量、$N_1$是属于类别$C_1$的样本的数量。
- $\mu^1=\frac{1}{N_1}\sum_{x^r\in C_1}x^r+\frac{1}{\sum_{x^u}P(C_1|x^u)}\sum_{x^u}P(C_1|x^u)x^u$,其中$x^r,x^u$分别指有标签的样本和无标签的样本
同理可知其它参数的计算和更新方法
返回第2步
理论上,上述步骤是可以收敛的,但参数$\theta$的初始化值会影响结果。其实上面的第2步是EM算法中的E,第3步是EM算法中的M。
理论推导
$\theta=\{P(C_1),P(C_2),\mu^1,\mu^2,\Sigma\}$
Maximum likelihood with labelled data
使得$logL(\theta)=\sum_{x^r}logP_\theta(x^r, \hat y^r)$最大(有一个Closed-form solution),其中每个有标注样本$x^r$的$P_\theta(x^r,\hat y^r)=P_\theta(x^r|\hat y^r)P(\hat y^r)$。
Maximum likelihood with labelled & unlabeled data
使得$logL(\theta)=\sum_{x^r}logP_\theta(x^r, \hat y^r)+\sum_{x^u}logP_\theta(x^u)$最大(该式并不是凹函数,所以需要迭代求解),其中每个无标注样本$x^u$的$P_\theta(x^u)=P_\theta(x^u|C_1)P(C_1)+P_\theta(x^u|C_2)P(C_2)$
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!