LSTM即Long Short-term Memory。
基本概念
前几篇文章提到的RNN都比较简单,可以任意读写memory,没有进一步对memory进行管理。现在常用的memory管理方式是LSTM。正如其名,LSTM是比较长的短期记忆,-是在short和term之间。前几篇提到的RNN在有新的输入时都会更新memory,这样的memory是非常短期的,而LSTM中可以有更久之前的memory。
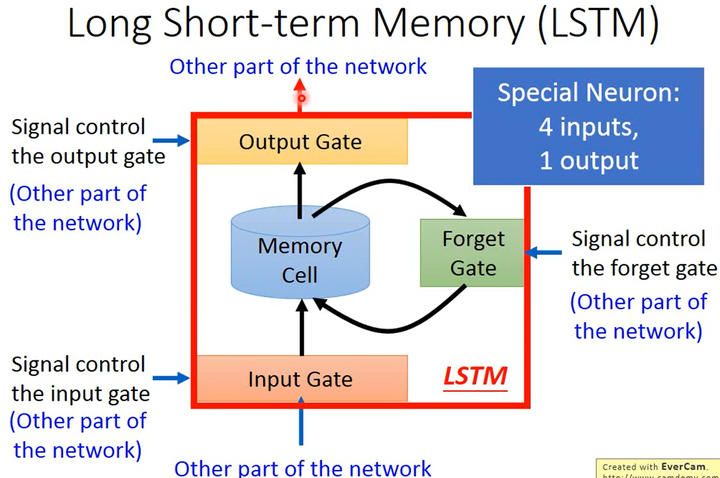
如上图所示,LSTM中有3个gate、4个输入(3个gate控制信号和1个想要写入memory cell的值)和1个输出:
- input gate:当某个neuron的输出想要被写进memory cell,它要先经过input gate。如果input gate是关闭的,则任何内容都无法被写入。input gate的关闭与否、什么时候开闭是由神经网络学习到的。
- output gate:output gate决定了外界是否可以从memory cell中读取数据。当output gate关闭的时候,memory里面的内容无法被读取。output gate的关闭与否、什么时候开闭也是由神经网络学习到的。
- forget gate:forget gate决定什么时候需要把memory cell里存放的内容忘掉,什么时候要保存。这也是由神经网络学习到的。
LSTM计算式
下图展示了LSTM的计算式。
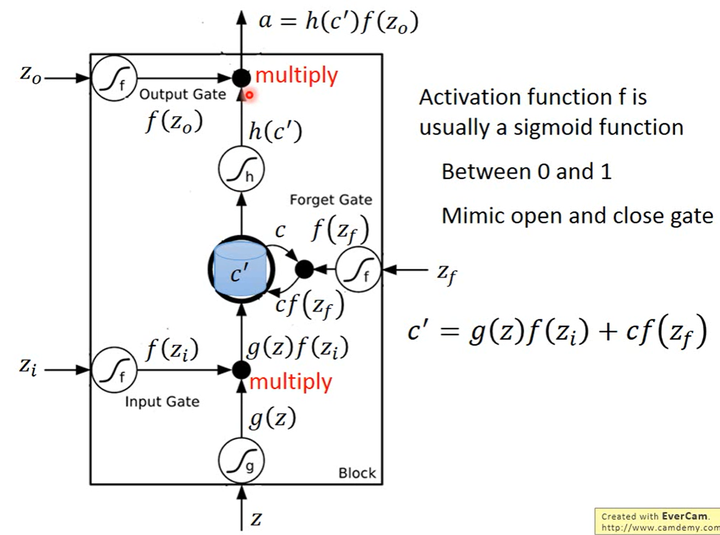
- $z$是想要被存到memory cell里的值
- $z_i$是input gate的控制信号
- $z_o$是output gate的控制信号
- $z_f$是forget gate的控制信号
- $a$是综合上述4个输入得到的输出值
$z$、$z_i$、$z_o$和$z_f$通过激活函数分别得到$g(z)$、$f(z_i)$、$f(z_o)$和$f(z_f)$,其中$z_i$、$z_o$和$z_f$的激活函数$f()$一般会选sigmoid函数,因为其输出在0~1之间,可表示gate的开启程度。
令$g(z)$与$f(z_i)$相乘得到$g(z)f(z_i)$,然后把原先存放在memory cell中的$c$与$f(z_f)$相乘得到$cf(z_f)$,两者相加得到存在memory cell中的新值$c’=g(z)f(z_i)+cf(z_f)$。
若$f(z_i)=0$,则相当于并不使用输入$z$更新memory;若$f(z_i)=1$,则相当于直接输入$g(z)$。
若$f(z_f)=1$,则不忘记memory cell中的原值$c$;若$f(z_f)=0$,则原值$c$将被遗忘清除。
可以看出,forget gate的逻辑与直觉是相反的,该控制信号打开表示记得原值,关闭却表示遗忘。这个gate取名为remember gate更好些。
此后,$c’$通过激活函数得到$h(c’)$,与output gate的$f(z_o)$相乘,得到输出$a=h(c’)f(z_o)$。
Apply LSTM to NN
上述的LSTM应该如何应用于神经网络呢?其实直接把LSTM作为1个神经元就可以了。假设输入层有2个标量输入$x_1,x_2$,隐藏层中有2个神经元,每个神经元输出1个标量,则其结构如下图所示。
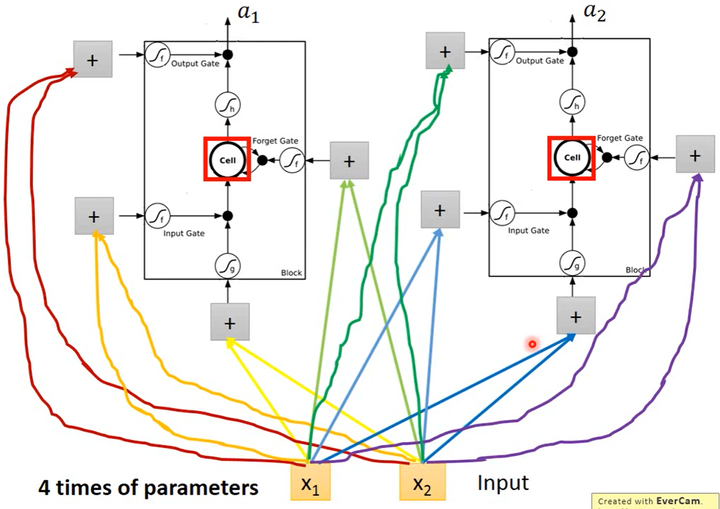
- 标量输入$x_1,x_2$乘以4个参数得到4个值,这4个值作为LSTM的4个input。
- 在普通的神经元中,1个input对应1个output;而在LSTM中4个input才产生1个output,并且所有的input都是不相同的。
- LSTM所需要的参数量是普通NN的4倍。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!