术语(Terminology)
Aggregation
Aggregation是Convolution在GNN中的推广。Aggregation就是在某一个layer中用某node及其neighbor的feature得到下一个layer中该node的feature。
Readout
Readout有点像是全连接在GNN中的推广。Readout就是汇总整个图的信息,最终得到一个特征来表示这整个图(Graph Representation)。
NN4G(Neural Network for Graph)
论文链接:https://ieeexplore.ieee.org/document/4773279
输入层
假如是一个化学分子,输入层的图中的结点就是一个原子。不同原子有不同的特征, 其特征可以是任何和原子相关的化学特征,所以需要embedding(将高维特征映射到低维特征),做完embedding也就得到了隐藏层$h^0$。
隐藏层$h^0$
如何做embedding呢?让原特征乘以embedding matrix就得到隐藏层$h^0$。如下图所示,以1个结点为例,输入层中结点$v_3$的特征是$x_3$,该结点embedding时的计算式为$h^0_3=\bar w_0\cdot x_3$。embedding后就得到了隐藏层$h^0$,然后再对隐藏层$h^0$进行Aggregation就得到了隐藏层$h^1$。
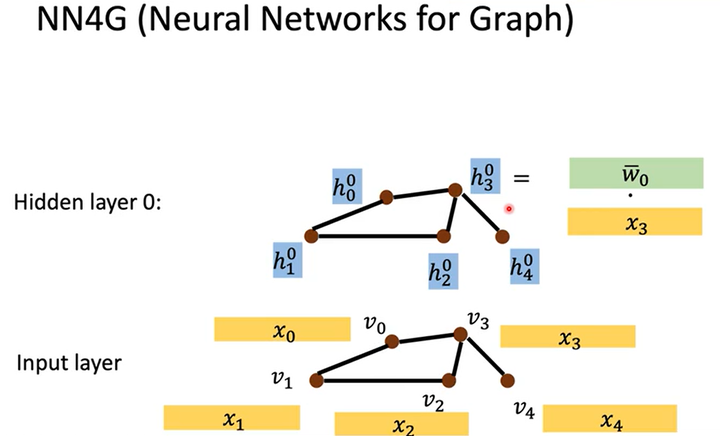
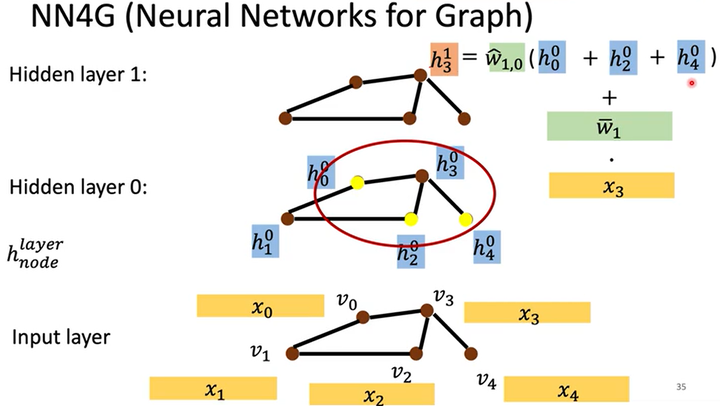
隐藏层$h^1$
如何做Aggregation呢?如下图所示,以1个结点为例,在隐藏层$h^0$中,结点$h^0_3$和$h^0_0,h^0_2,h^0_4$3个结点相邻,则Aggregation时计算式为$h^1_3=\hat w_{1,0}(h^0_0+h^0_2+h^0_4)+\bar w_1\cdot x_3$。经过多次Aggregation,最后需要Readout。
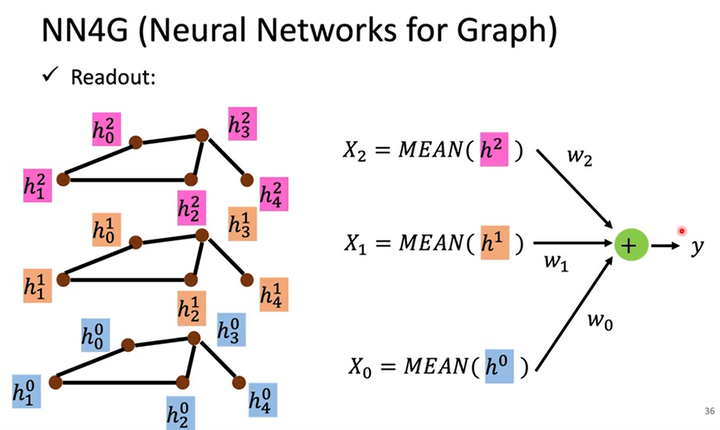
Readout
如何做Readout呢?如下图所示,假设有3个隐藏层,那Readout的计算式为$y=MEAN(h^0)+MEAN(h^1)+MEAN(h^2)$。
DCNN(Diffusion-Convolution Neural Network)
论文链接:https://arxiv.org/abs/1511.02136
输入层
假如我们有1个和上例中(NN4G)一样的输入图。
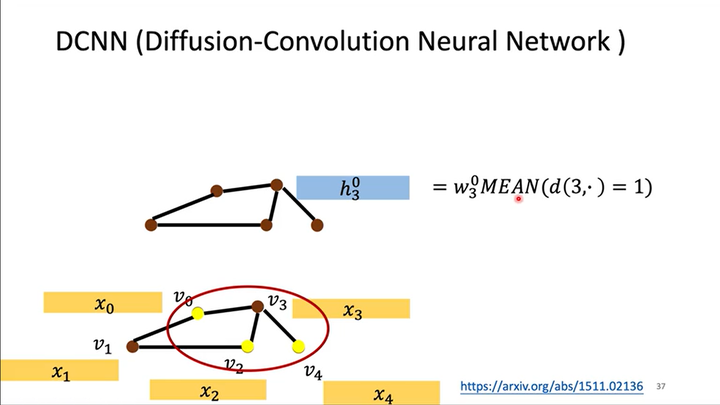
隐藏层$h^0$
如下图所示,从输入层到隐藏层$h^0$的计算式为$h^0_3=w^0_3MEAN(d(3,\cdot)=1)$,其中$d(3,\cdot)=1$表示所有与结点$x_3$距离为1的输入层结点的特征。
隐藏层$h^1$
如下图所示,从隐藏层$h^0$到隐藏层$h^1$的计算式为$h^1_3=w^1_3MEAN(d(3,\cdot)=2)$,其中$d(3,\cdot)=2$表示所有与结点$x_3$距离为2的输入层结点的特征。
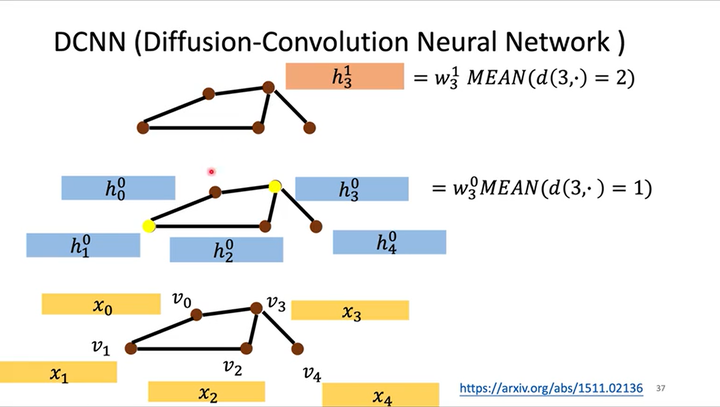
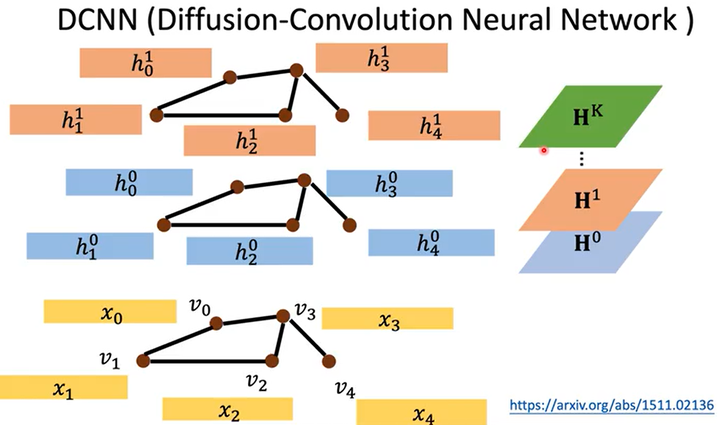
以此类推,叠加k个隐藏层后就可以获取各结点k范围内的信息。如下图所示,令1个隐藏层中多个结点的特征形成矩阵(1行是1个结点的特征),多个隐藏层的特征就形成多个通道$H^0,H^1,\dots,H^k$。
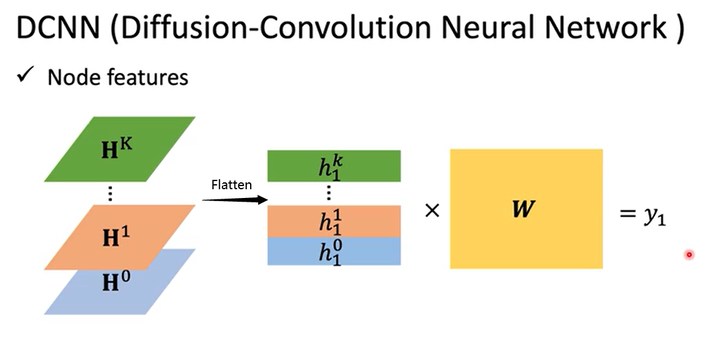
Node features
如何表达整个图的特征呢?如下图所示,将每个通道的特征flatten,然后再乘以参数$w$得到$y_1$即可。
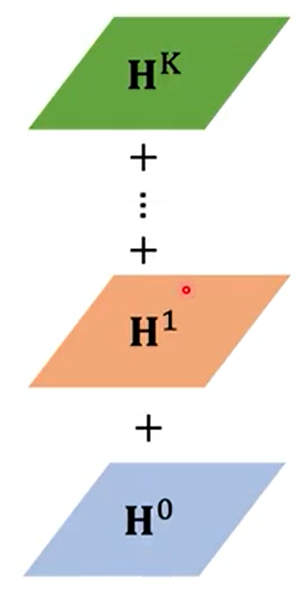
也有其它做法,ICLR2018中DGC(Diffusion Graph Convolution)不是flatten,而是相加,如下图所示。
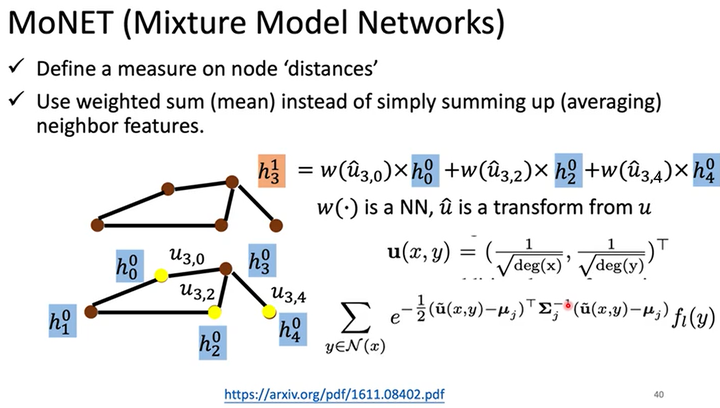
MoNET(Mixture Model Networks)
NN4G、DCNN都是将邻居结点的特征直接相加,并没有考虑各个邻居结点特征的重要性,而MoNET考虑了这个问题。
论文链接:https://arxiv.org/abs/1611.08402
MoNET定义了结点距离的概念,基于结点距离表示各个邻居结点特征的重要性然后对各个邻居结点进行加权求和,而不是简单地取均值或求和。
如下图所示,假如我们有和上例一样的输入图,隐藏层$h^0$中结点$v_3$的特征为$h^0_3$,结点$v_3$和结点$v_0$的距离为$u_{3,0}$。
定义结点$x,y$的距离$u(x,y)=(\frac{1}{\sqrt{deg(x)}},\frac{1}{\sqrt{deg(y)}})^T$,其中$deg(x)$表示结点$x$的度(degree,度是连接到每个节点的边的数量)。
GraphSAGE
SAmple and aggreGatE(GraphSAGE),在transductive和inductive setting上都能work。
论文链接:https://arxiv.org/abs/1706.02216
GraphSAGE的Aggregation除了mean,还有max pooling和LSTM。LSTM用来处理序列数据,但图中结点的邻居并没有序列关系,但如果每次在邻居中随机取样出不同顺序,那也许可以忽略顺序学习到顺序无关的信息。
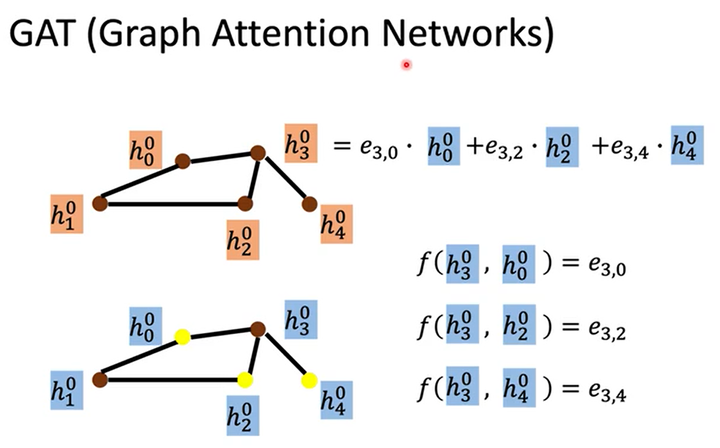
GAT(Graph Attention Networks)
论文链接:https://arxiv.org/abs/1710.10903
GAT不只是做加权求和(weighted sum),而其中的weight是通过学习得到的,方法就是对邻居做attention。
假如我们有1个和上例中(NN4G)一样的输入图。在做aggregation时,我们通过函数$f$计算各个邻居结点$v_0,v_2,v_4$对结点$v_3$的重要性,然后做加权求和。
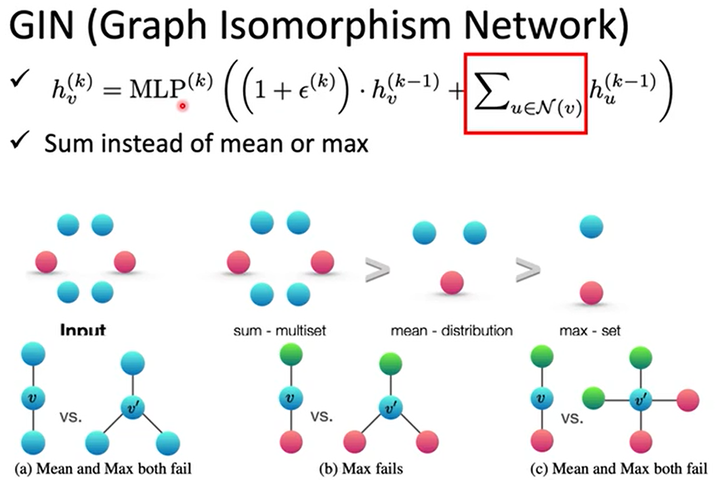
GIN(Graph Isomorphism Network)
这篇论文偏理论,证明出有些方法是work的,有些是不会work的。
比如提取特征时不要用mean或max(在一些情况下会fail),要用sum,如下图所示。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!