卷积神经网络(CNN)常常被用来做图像处理,当然也可以用一般的神经网络,那它们各自有什么优缺点呢?
FNN用于图片处理的缺点
使用一般的全连接前馈神经网络(FNN)处理图片时的缺点:
需要很多的参数
假设有一张尺寸100×100的图片(尺寸已经算很小了),那输入层就有100×100×3=30K个像素,假设第一个隐藏层有1K个神经元(一个神经元包含30K个参数),这就已经需要30M个参数了……
该架构中每个神经元就是一个分类器,这是没必要的
第一个隐藏层作为最基础的pattern分类器(比如判断有无绿色、边缘等),第二个隐藏层基于第一个隐藏层继续做pattern分类(比如木头、肉类),以此类推……
按照人类的直观理解,我们不是像全连接神经网络一样去处理图片的。具体来看,有哪些方面呢?
图片的一些性质
结合全连接前馈神经网络的缺点和人类对图片的直观理解,可以得到下述图片的3个性质。
性质1:Some patterns are much smaller than the whole image.
在识别某个模式(pattern)时,一个神经元并不需要图片的所有像素点。对于一张人类全身照的图片,我们只需要看到头部而非整张图片就可以判断它是一个人脸。所以我们应该是可以用少量参数去识别这些pattern的。

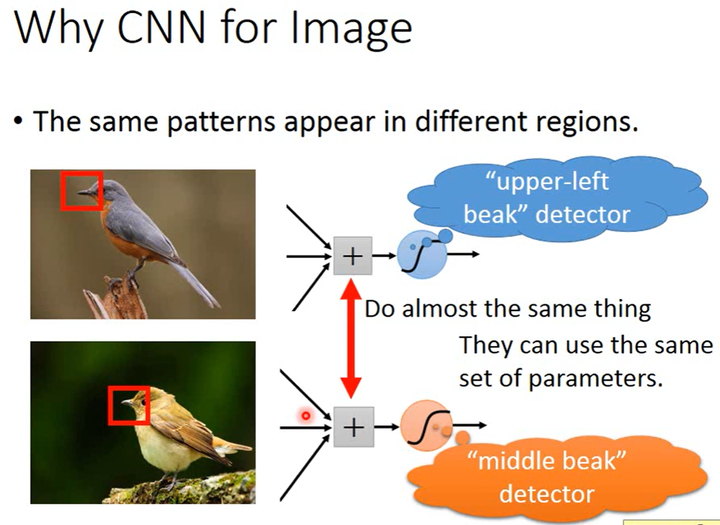
性质2:The same patterns appear in different regions.
比如说人脸可以在图片的中间区域,也可以在图片的某个角落区域。所以识别不同区域中的相同pattern的多个分类器(或detector)应该用同一组参数或者共享参数。
性质3:Subsampling the pixels will not change the object
将图片缩小/下采样,并不会影响我们理解图片。所以我们可以通过将图片变小,进而用更少的参数处理图片。

CNN架构说明
2014年在ECCV上提出,针对上述的图片的3个性质,确定了CNN的架构如下。
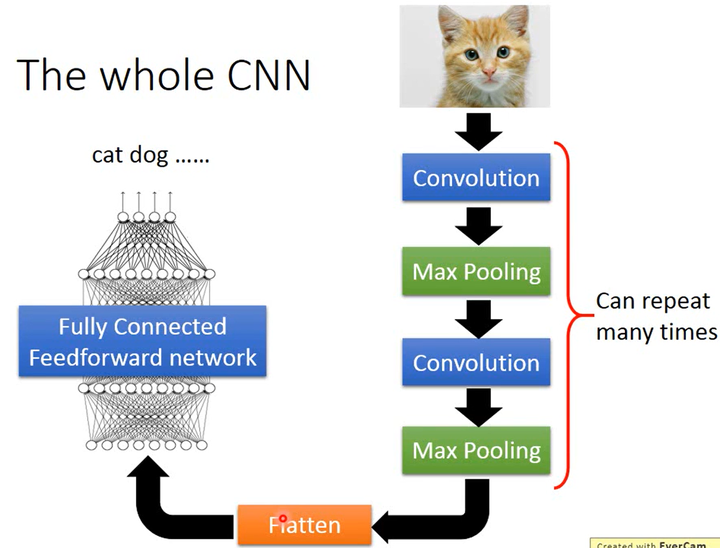
如上图所示,图片经过卷积层然后进行最大池化(max pooling),这个步骤可以进行多次;然后将数据展开(Flatten),然后将数据传进全连接前馈网络得到最后的图片分类结果。
CNN架构作用探析
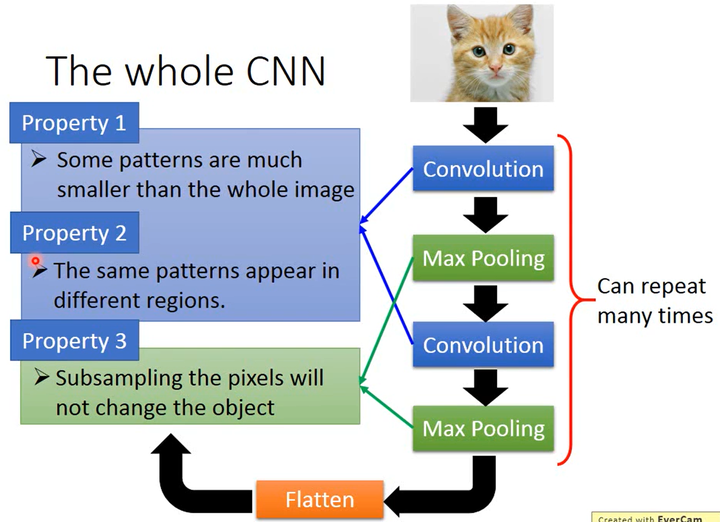
如上图所示,卷积是针对了图片的性质1和性质2,最大池化是针对了图片的性质3。
卷积(Convolution) ★
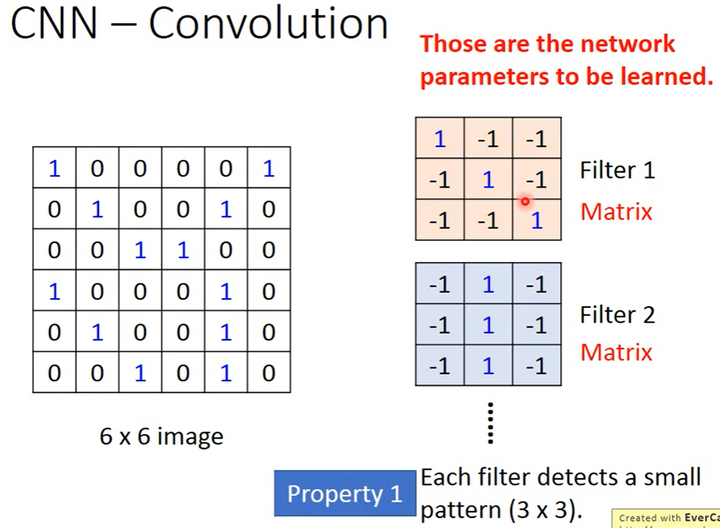
假设有一张6×6的二值图,即一个6×6的矩阵。
卷积核(Filter)
神经元就是一个计算/函数,卷积核其实就是神经元。
如下图所示,1个卷积层可以有多个卷积核,矩阵里元素的值就是需要通过学习得到的参数。
因为这里的输入是一个矩阵,所以卷积核也是1个矩阵(卷积核的通道数等于输入的通道数)。
假设卷积核大小是3×3,这对应了图片的性质1,即用小的卷积核识别一个小的pattern。
怎么做卷积
如下图所示
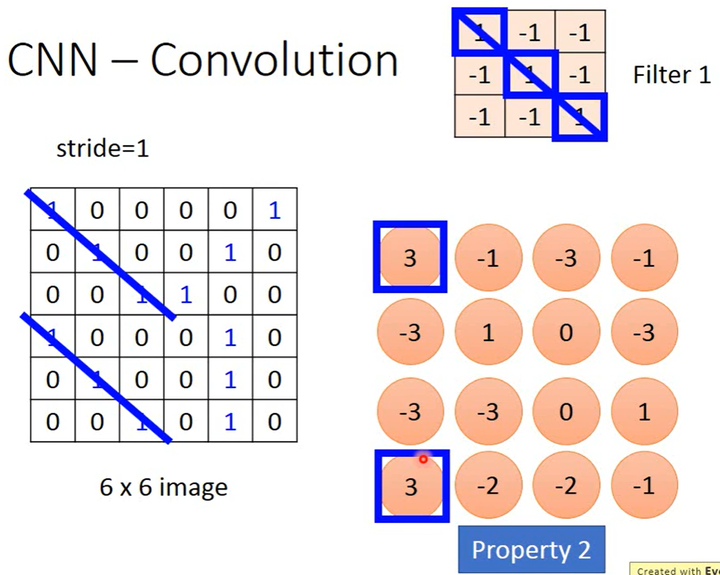
卷积区域
根据该卷积核的大小(以3×3为例),选择图片中相同大小的区域进行卷积。
卷积的计算方法
从图片中扫描得到的3×3矩阵和卷积核的3×3矩阵,这2个矩阵相同位置的元素相乘可以得到9个值并求和(也就是内积)得到1个值,这就是1次卷积操作。
卷积顺序和方向
卷积核按照从左到右、从上到下的顺序,从图片左上角开始移动,移动步长(stride)可以设置(以1为例)。在扫描到的每个区域中,都进行1次卷积。1个卷积核移动结束后,则得到1个新的矩阵(大小为4×4),即1个卷积核的输出是1个矩阵。
卷积层有多个卷积核,每个卷积核都按照该方式进行卷积得到多个矩阵,这些矩阵合起来就形成了1个卷积层的特征图(Feature Map),这个特征图也就是卷积层的输出。
卷积层特征图的通道数等于该卷积层中卷积核的数量,即某卷积层有多少个卷积核,那该卷积层的特征图就有多少个通道。
卷积的作用
在上图中,卷积核1的“对角线”的值都是1,就可以识别出图片中哪个区域具有“对角线”。在上图得到的4×4矩阵中,我们可以看到左上角和左下角3个元素的值为3,即有“对角线”。这对应了图片的性质2,我们用1个filter/1组参数识别了不同位置的相同pattern。
卷积核是矩阵还是张量
卷积核可以是矩阵,也可以是张量,要根据其输入决定。
卷积核的通道数等于其所在卷积层输入的通道数(即其所在卷积层前一层的特征图的通道数),即单个卷积核会考虑输入的所有通道。
假如输入是一张RGB图片(大小为3×N×N,即有3个通道、每个通道中矩阵大小为N×N),那卷积核就是1个张量(大小为3×M×M,即有3个通道、每个通道中矩阵大小为M×M),卷积计算方法和上面一样是求内积(两个3×M×M的张量求内积)。
卷积中如何做梯度下降
因为一个卷积核要对图片的不同区域进行多次卷积,每次卷积都会有一个梯度,最终把这些梯度取平均值就好了。
大概这么个意思,实操中这种底层的东西不需要我们实现。
Convolution VS Fully Connected
其实,卷积核就是一个神经元,它相当于全连接层中的神经元并没有全连接(没有使用图片的所有像素,当然这样的层也就不能称为全连接层了),这样有两个好处
模型的参数更少
如下图所示,因为没有使用所有像素、不是全连接,因此需要的参数更少。
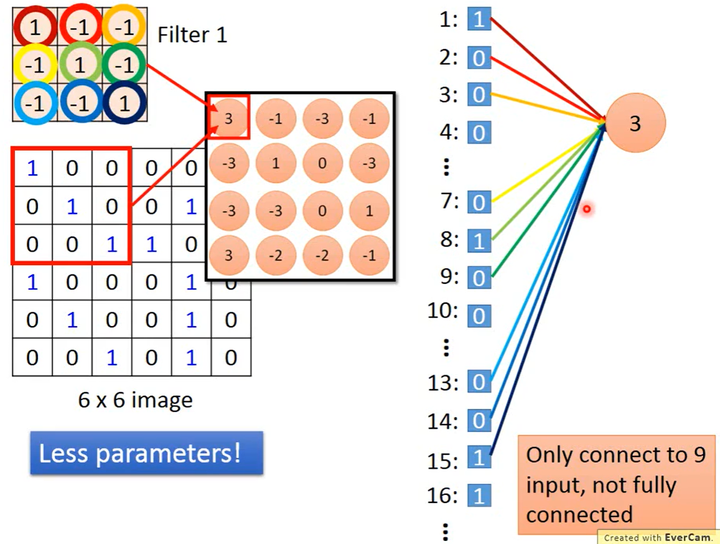
参数共享
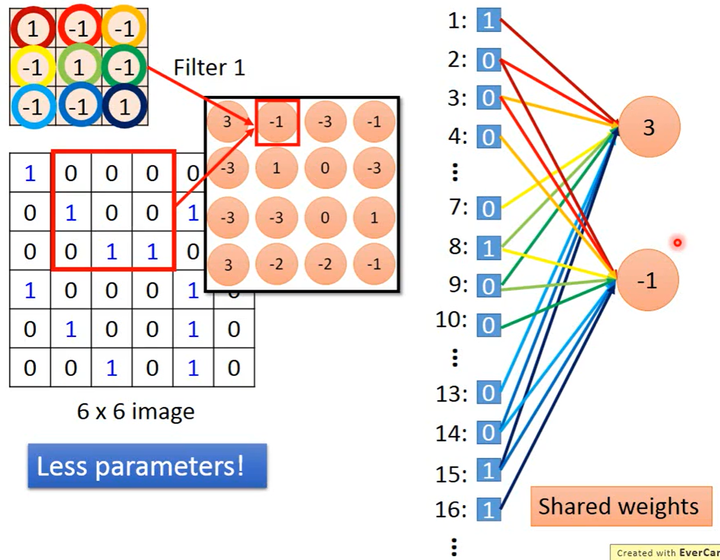
如下图所示,因为用同1个卷积核在图片的不同区域做卷积,即用1组参数对不同区域的像素进行计算,得到了多个值、达成了多个神经元的效果,实现了参数共享。比如下图中神经元“3”处理图片第1个像素和神经元“-1”处理图片第2个像素就使用了同一个参数“1”(卷积核的第1个参数)。
因为实现了参数共享,卷积就比全连接进一步减少了参数量。
最大池化(Max Pooling)
最大池化是一种下采样(Subsample),下采样不一定要取最大值,也可以取平均值。
怎么做最大池化
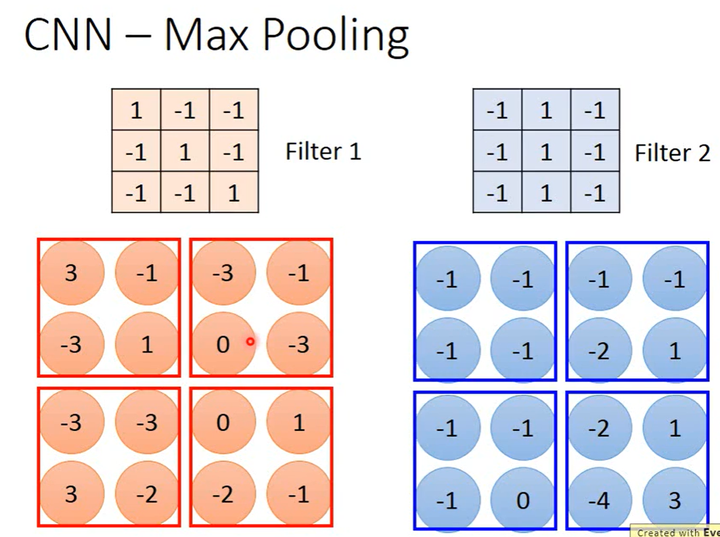
如上图所示,假如某Max Pooling层的上1层是1个有2个卷积核的卷积层,该卷积层的输出是一个张量(大小为2×4×4,即2个通道、每个通道中矩阵的大小为4×4)。
对于输入中的每个通道,Max Pooling将4×4的矩阵划分成4个2×2的子矩阵(子矩阵大小可以人为设定),只取出每个子矩阵中的最大值就得到一个2×2的矩阵。又因为该Max Pooling层的输入有2个通道,所以其输出就是一个大小为2×2×2的张量。
取最大值的话,该怎么微分?
见笔记“Tips for Training DNN”Maxout部分,Max Pooling和Maxout其实是一样的。
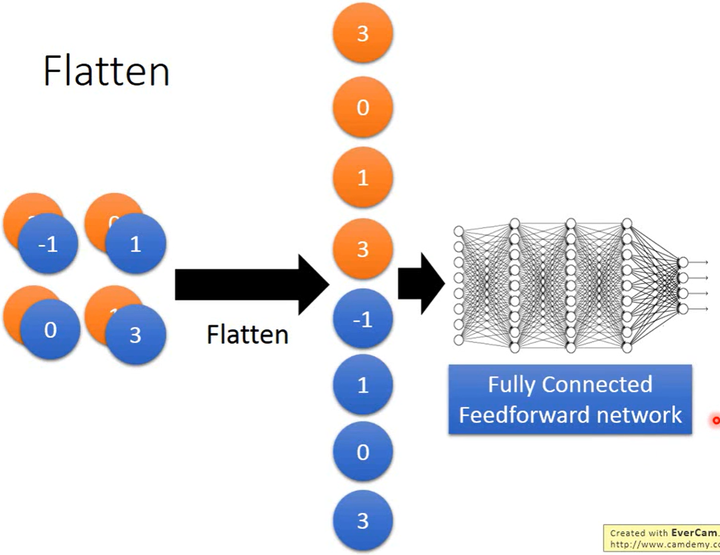
Flatten & FNN
经过一系列的卷积和最大池化,将得到的特征图展开排列,作为FNN的输入,最后输出结果。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!