[TOC]
链式法则(Chain Rule)
- $z=h(y),y=g(x)\to\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}$
- $z=k(x,y),x=g(s),y=h(s)\to\frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds}$
反向传播算法(Backpropagation)
变量定义
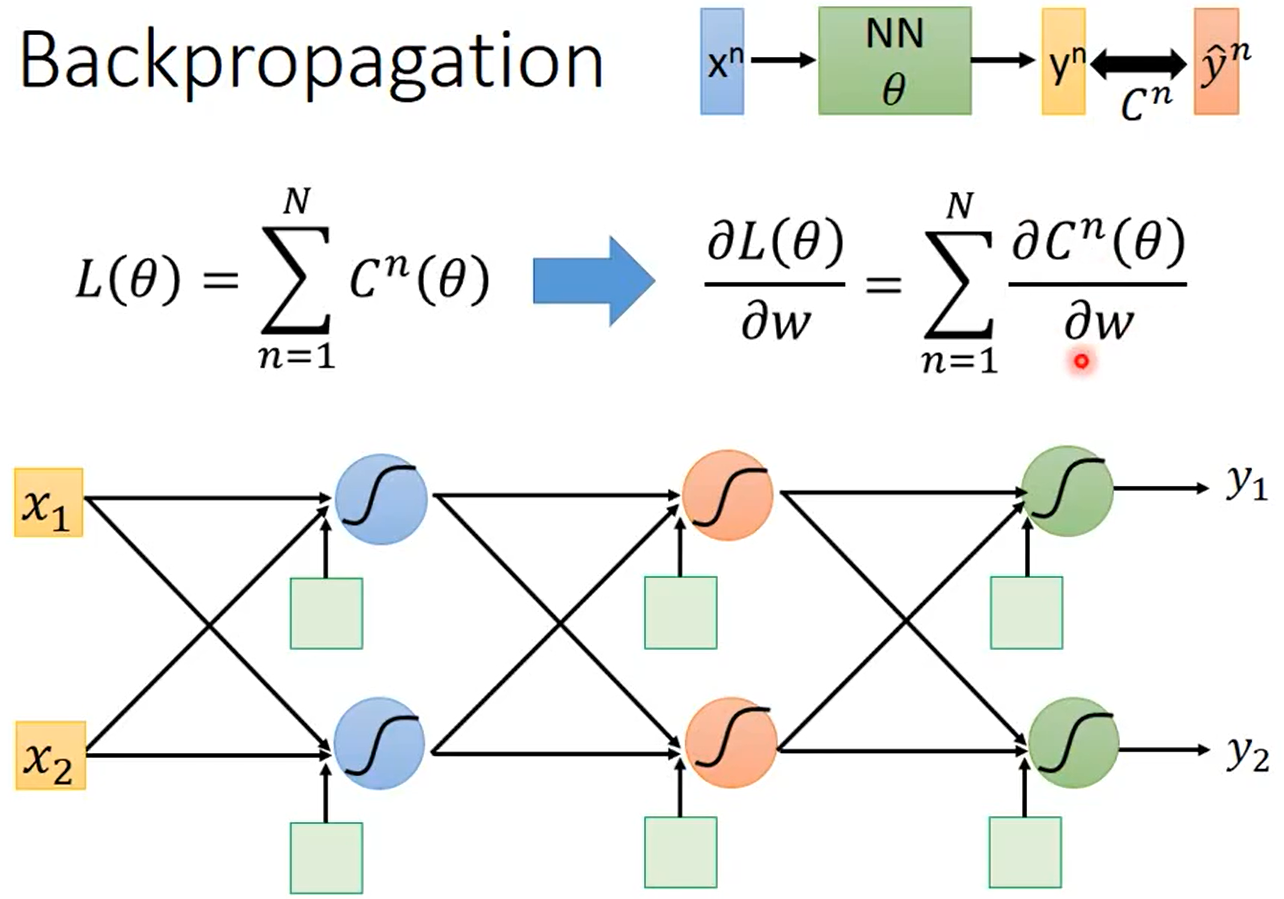
如下图所示,设神经网络的输入为$x^n$,该输入对应的label是$\hat y^n$,神经网络的参数是$\theta$,神经网络的输出是$y^n$。
整个神经网络的Loss为$L(\theta)=\sum_{n=1}^{N}C^n(\theta)$。假设$\theta$中有一个参数$w$,那$\frac{\partial L(\theta)}{\partial w}=\sum^N_{n=1}\frac{\partial C^n(\theta)}{\partial w}$。
一个神经元的情况
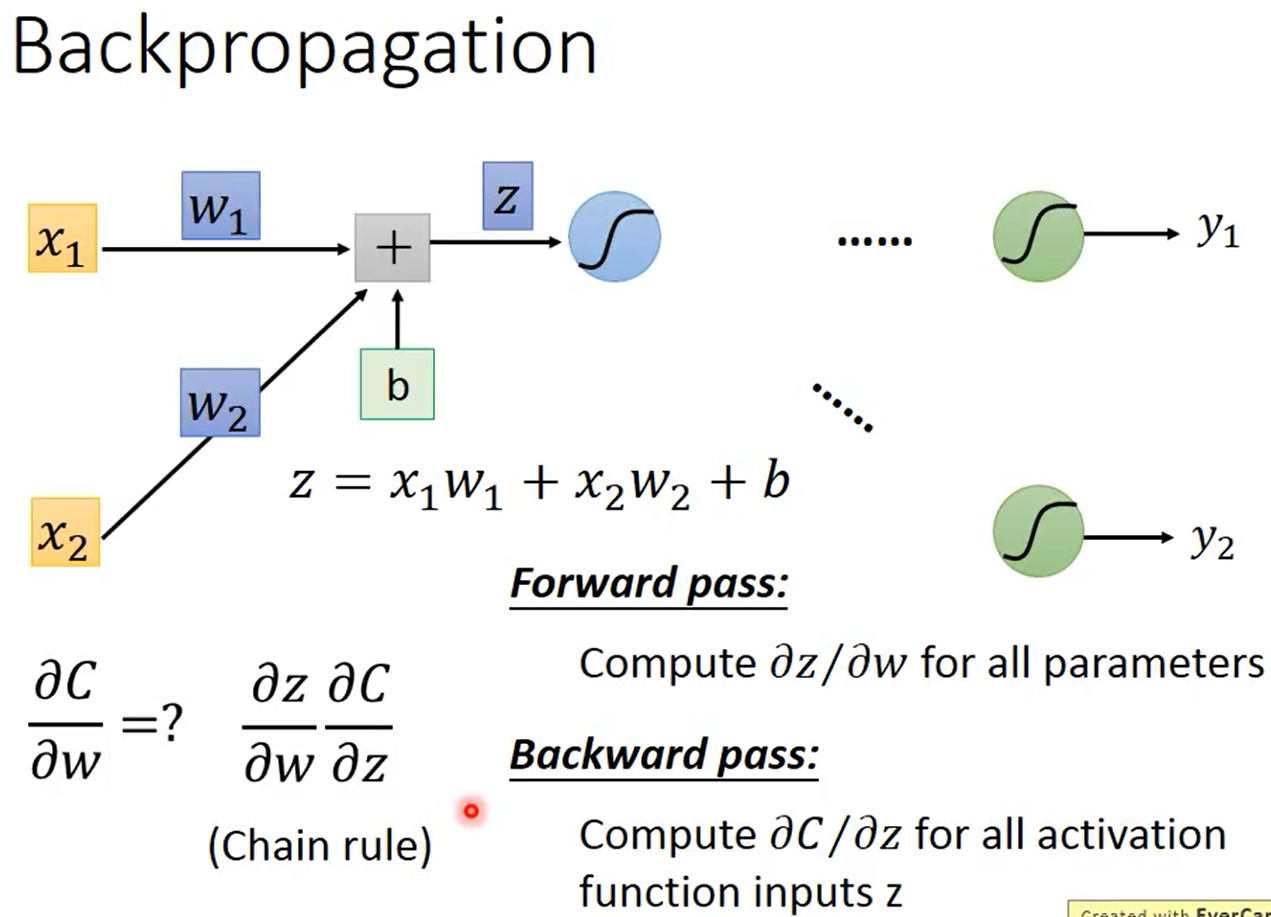
如下图所示,$z=x_1w_1+x_2w_x+b$,根据链式法则可知$\frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z}$,其中为所有参数$w$计算$\frac{\partial z}{\partial w}$是Forward Pass、为所有激活函数的输入$z$计算$\frac{\partial C}{\partial z}$是Backward Pass。
Forward Pass
Forward Pass是为所有参数$w$计算$\frac{\partial z}{\partial w}$,它的方向是从前往后算的,所以叫Forward Pass。
以一个神经元为例,因为$z=x_1w_1+x_2w_x+b$,所以$\frac{\partial z}{\partial w_1}=x_1,\frac{\partial z}{\partial w_2}=x_2$,如下图所示。
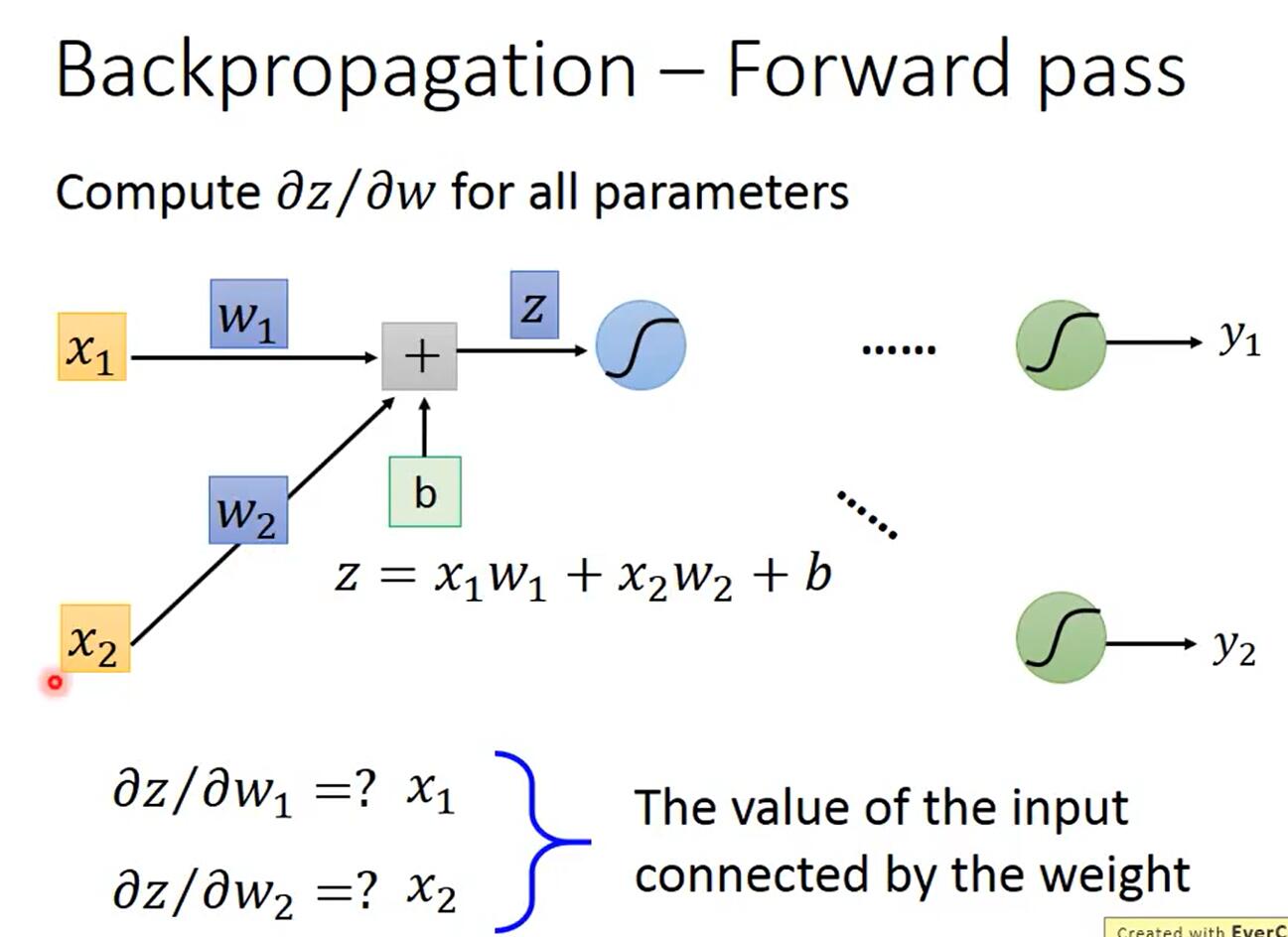
规律是:该权重乘以的那个输入的值。所以当有多个神经元时,如下图所示。

Backward Pass
Backward Pass是为所有激活函数的输入$z$计算$\frac{\partial C}{\partial z}$,它的方向是从后往前算的,要先算出输出层的$\frac{\partial C}{\partial z}$,再往前计算其它神经元的$\frac{\partial C}{\partial z}$,所以叫Backward Pass。

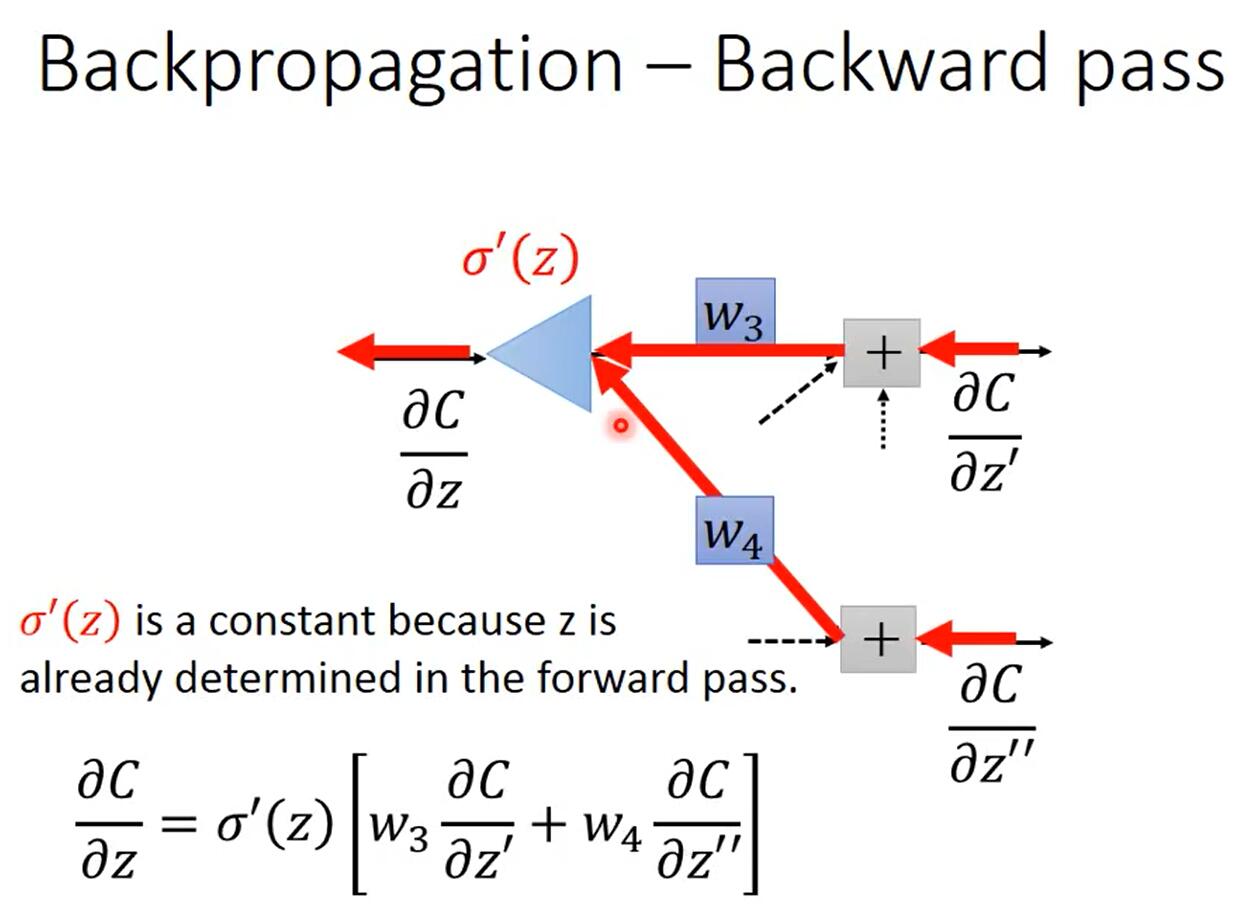
如上图所示,令$a=\sigma(z)$,根据链式法则,可知$\frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a}$,其中$\frac{\partial a}{\partial z}=\sigma’(z)$是一个常数,因为在Forward Pass时$z$的值就已经确定了,而$\frac{\partial C}{\partial a}=\frac{\partial z’}{\partial a}\frac{\partial C}{\partial z’}+\frac{\partial z’’}{\partial a}\frac{\partial C}{\partial z’’}=w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z’’}$,所以$\frac{\partial C}{\partial z}=\sigma’(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z’’}]$。
对于式子$\frac{\partial C}{\partial z}=\sigma’(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z’’}]$,我们可以发现两点:
$\frac{\partial C}{\partial z}$的计算式是递归的,因为在计算$\frac{\partial C}{\partial z}$的时候需要计算$\frac{\partial C}{\partial z’}$和$\frac{\partial C}{\partial z’’}$。
如下图所示,输出层的$\frac{\partial C}{\partial z’}$和$\frac{\partial C}{\partial z’’}$是容易计算的。
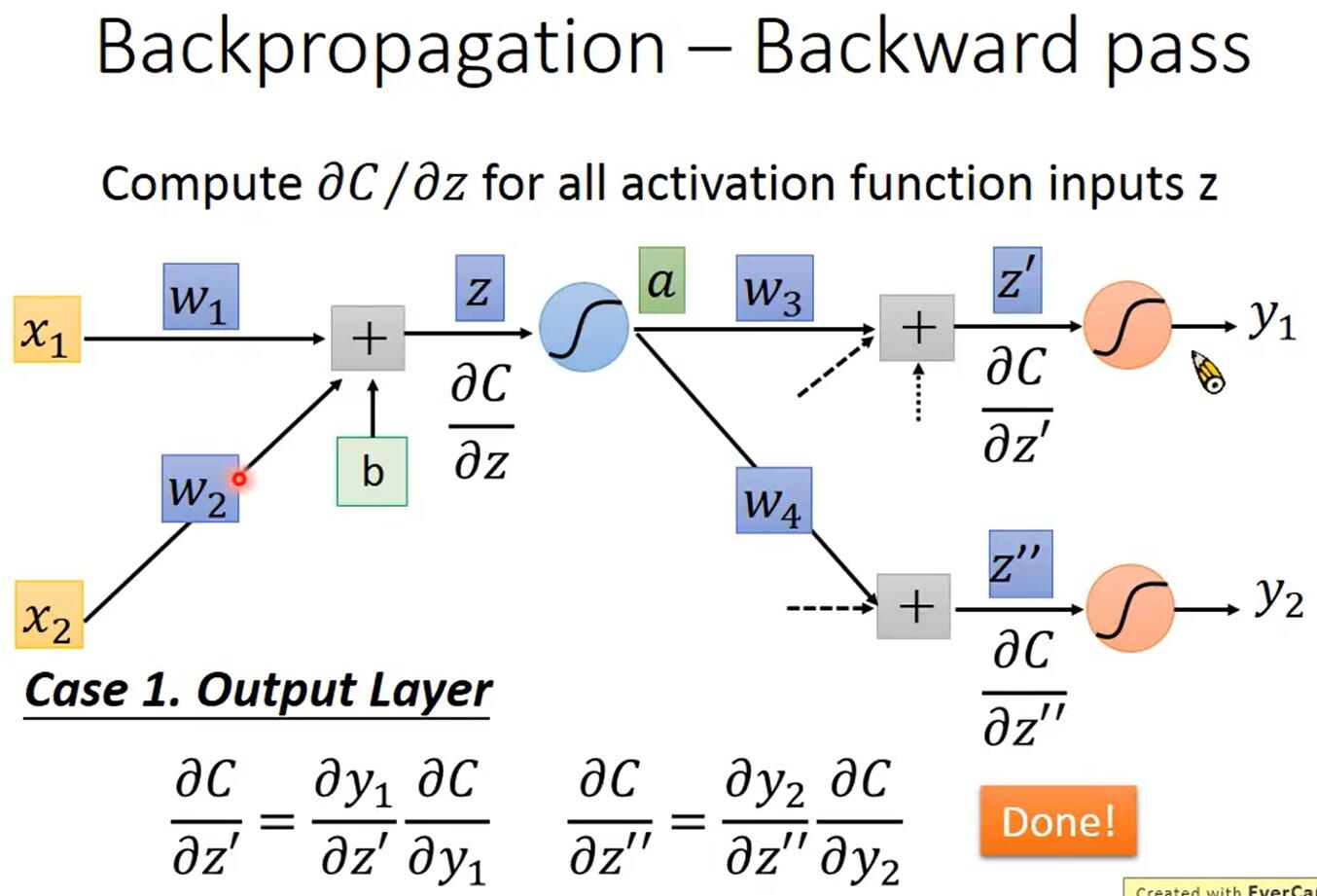
$\frac{\partial C}{\partial z}$的计算式$\frac{\partial C}{\partial z}=\sigma’(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z’’}]$是一个神经元的形式
如下图所示,只不过没有嵌套sigmoid函数而是乘以一个常数$\sigma’(z)$,每个$\frac{\partial C}{\partial z}$都是一个神经元的形式,所以可以通过神经网络计算$\frac{\partial C}{\partial z}$。
总结
- 通过Forward Pass,为所有参数$w$计算$\frac{\partial z}{\partial w}$;
- 通过Backward Pass,为所有激活函数的输入$z$计算$\frac{\partial C}{\partial z}$;
- 最后$\frac{\partial C}{\partial w}=\frac{\partial C}{\partial z}\frac{\partial z}{\partial w}$,也就求出了梯度。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭咸鱼
知乎(zhihu.com):@臭咸鱼
博客园(cnblogs.com):@臭咸鱼
B站(bilibili.com):@绝版臭咸鱼
微信公众号:@臭咸鱼
转载请注明出处,欢迎讨论和交流!