美国人口指数增长模型拟合

Posted on | | Visitors:
Words count in article: 376 字 | Reading time ≈ 2 分

假设

美国人口数满足指数增长模型$x(t)=x_0e^{rt}$，其中$x(t)$表示第$t$年的人口数，$x_0$表示第0年的人口数，即人口数初值。

思路

$ x(t) = x_0e^{rt} \ \Rightarrow \ ln \,x(t)=rt+ln\,x_0 \,\Rightarrow Y=ln \,x(t)a_1t+a_2$ ，

其中$Y=ln\,x(t)$，$a_1=r$，$a_2=ln\,x_0$。

如上，将指数函数转化为线性函数，利用线性函数进行拟合，再将线性函数转化为指数函数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
t  = 1790 : 10 : 1900; % 时间
p = [3.9   5.3    7.2    9.6 ...
      12.9 17.1  23.2  31.4 ...
      38.6  50.2 62.9  76.0];  % 人口数

  Y = log(p); % 转换为线性
  X = t; % 不用X直接用t也可以
  a = polyfit(X, Y, 1); % X,Y线性拟合
  x0 = exp(a(2)); %
  r = a(1);
  ti = 1790:1900; % 曲线的横坐标
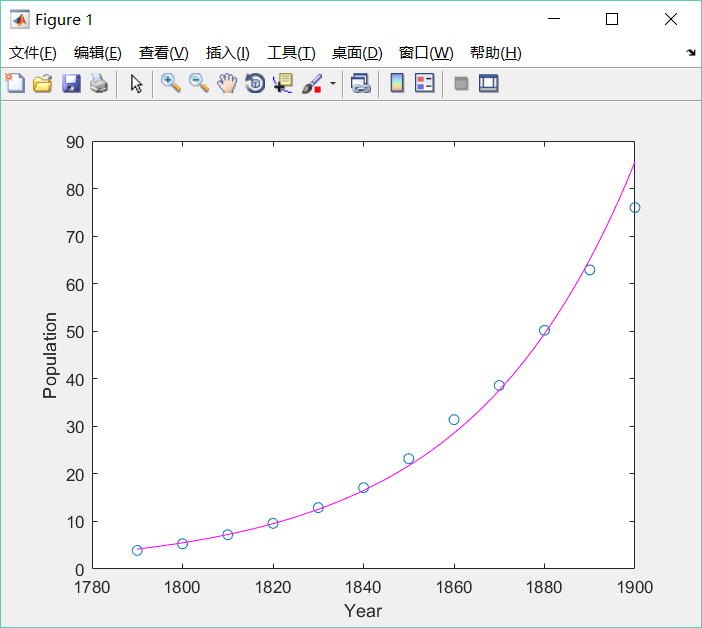
  pti = x0*exp(r*ti); % 曲线纵坐标，即拟合结果
  plot(t, p, 'o', ti, pti, 'm'); % 原数据与拟合结果对比
  xlabel('Year');
  ylabel('Population');

结果

美国人口指数增长模型拟合.png

可以看到，前期拟合结果较好，但是1890年到1900年曲线与原数据相比偏高。

原因是人口数并不完全符合指数增长模型，人口并不能完全地按照“J”型曲线增长，而应该是“S”型曲线。物种竞争嘛，所以刚开始的假设是不合理的，可以再进行优化。

作者：@臭咸鱼

本文为作者原创，转载请注明出处：https://chouxianyu.github.io

欢迎讨论和交流!